加法定理から、様々な公式が導かれます。数多くの公式が出てきますが、これらをまる覚えするのではなく、導き方を理解するようにしてください。
また、以下で紹介する公式の中でも、「２倍角の公式」と「三角関数の合成」と呼ばれるものが使用頻度が多いので、まずそれらから理解するようにしてください。
２倍角の公式
加法定理
\begin{align*}
(1)\ &\sin( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
(2)\ &\cos( \alpha + \beta ) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \\
(3)\ &\tan( \alpha + \beta ) = \frac{ \tan \alpha + \tan \beta }{ 1 – \tan \alpha \tan \beta}
\end{align*}
に対して、\( \beta \)を\( \alpha \)に置き換えたものが２倍角の公式です。
(1)
\begin{align*}
&\sin ( \alpha + \alpha ) = \sin \alpha \cos \alpha + \cos \alpha \sin \alpha \\
&\Leftrightarrow \ \sin 2 \alpha = 2 \sin \alpha \cos \alpha
\end{align*}
(2)
\begin{align*}
&\cos ( \alpha + \alpha ) = \cos \alpha \cos \alpha – \sin \alpha \sin \alpha \\
&\Leftrightarrow \ \cos 2 \alpha = \cos^2 \alpha – \sin^2 \alpha
\end{align*}
また、\( \sin^2 \alpha + \cos^2 \alpha = 1 \)であるので、
\[ \sin^2 \alpha = 1 – \cos^2 \alpha \]
または
\[ \cos^2 \alpha = 1 – \sin^2 \alpha \]
と表せます。
これを用いると、\( \cos 2 \alpha \)は、以下のように\( \cos \)のみ、あるいは\( \sin \)のみで表せます。
つまり
\[ \cos 2 \alpha = 2 \cos^2 \alpha – 1 \]
または
\[ \cos 2 \alpha = 1 – 2 \sin^2 \alpha \]
と表せます。
(3)
\begin{align*}
&\tan( \alpha + \alpha ) = \frac{ \tan \alpha + \tan \alpha }{ 1 – \tan \alpha \tan \alpha } \\
&\Leftrightarrow \tan 2 \alpha = \frac{ 2 \tan \alpha }{ 1 – \tan^2 \alpha }
\end{align*}
上記の結果をまとめておきます。
３倍角の公式
２倍角の公式では、加法定理に登場する\( \beta \)を\( \alpha \)に置き換えましたが、３倍角の公式では、\( \beta \)を\( 2\alpha \)に置き換えます。
（\( \tan \)の３倍角の公式については使うことがほぼありませんので省略します。）
(1)
\[ \sin ( \alpha + 2 \alpha ) = \sin \alpha \cos 2 \alpha + \cos \alpha \sin 2 \alpha \]
倍角公式を用いて、\( \cos 2 \alpha, \sin 2 \alpha \)を書き換えると
\begin{align*}
\sin 3 \alpha &= \sin \alpha (1 – 2 \sin^2 \alpha) + \cos \alpha \cdot 2 \sin \alpha \cos \alpha \\
&= \sin \alpha – 2 \sin^3 \alpha + 2 \sin \alpha \cos^2 \alpha \\
&= \sin \alpha – 2 \sin^3 \alpha + 2 \sin \alpha ( 1 – \sin^2 \alpha ) \\
&= 3 \sin \alpha – 4 \sin^3 \alpha
\end{align*}
(2)
\[ \cos ( \alpha + 2 \alpha ) = \cos \alpha \cos 2 \alpha – \sin \alpha \sin 2 \alpha \]
(1)と同様に倍角公式を用いて、\( \cos 2 \alpha, \sin 2 \alpha \)を書き換えると
\begin{align*}
\cos 3 \alpha &= \cos \alpha (2 \cos^2 \alpha – 1) – \sin \alpha \cdot 2 \sin \alpha \cos \alpha \\
&= 2 \cos^3 \alpha – \cos \alpha – 2 \sin^2 \alpha \cos \alpha \\
&= 2 \cos^3 \alpha – \cos \alpha – 2 (1 – \cos^2 \alpha) \cos \alpha \\
&= 2 \cos^3 \alpha – \cos \alpha – 2 \cos \alpha + 2 \cos^3 \alpha \\
&= 4 \cos^3 \alpha – 3 \cos \alpha
\end{align*}
三角関数の合成
加法定理を逆に見ると、関数\( y = a \sin x + b \cos x \)を\( y = A \sin (x + \alpha ) \)の形に書き換えることができます。
また、書き換えることで、２ヶ所にあった変数\( x \)が１ヶ所にまとめることができ、関数の様子がわかりやすくなり、最大値・最小値を求めることやグラフが描くことが簡単にできるようになります。
ここでは、\( y = \sqrt{3} \cos x + \sin x \)を書き換えていきます。
加法定理
\[ \sin( \alpha + x ) = \sin \alpha \cos x + \cos \alpha \sin x \]
の\( \sin x, \cos x \)の係数をそれぞれ２乗し、和を取ると
\[ \sin^2 \alpha + \cos^2 \alpha = 1 \]
であるから
もし、関数\( y = \sqrt{3} \cos x + \sin x \)の\( \sin x, \cos x \)の係数をそれぞれ２乗し、和を取り、１になるならば、加法定理をいままでと逆にみることで、\( \sin (x + \alpha) \)の形に表すことができます。
いま、\( \sin x, \cos x \)の係数の２乗の和は
\[ (\sqrt{3})^2 + 1^2 = 4 \]
この式の両辺を４で割ると
\[ (\frac{\sqrt{3}}{2})^2 + (\frac{1}{2})^2 = 1 \]
と書くことができます。
つまり、関数\( y = \sqrt{3} \cos x + \sin x \)の係数がいまの\( \frac{1}{2} \)であれば係数の２乗の和が１であったということです。
そこで、２乗して１になるように、\( \sqrt{3} \cos x + \sin x \)を２でくくります。
\[ \sqrt{3} \sin x + \cos x = 2( \frac{ \sqrt{3} }{2} \cos x + \frac{1}{2} \sin x ) \]
このようにすることで（ ）の中の\( \sin x ,\cos x \)の係数の２乗の和が１となります。
ここで\(\sin x, \cos x \)の係数について、（ ）の中の式と加法定理の右辺を見比べます。
\begin{align*}
&\underline{ \frac{ \sqrt{3} }{2} } \cos x + \underline{ \frac{1}{2} } \sin x \\
&\underline{ \sin \alpha } \cos x + \underline{ \cos \alpha } \sin x
\end{align*}
ここから
\begin{align*}
\sin \alpha = \frac{ \sqrt{3} }{2} \\
\cos \alpha = \frac{1}{2}
\end{align*}
となるので、\( \alpha = \frac{ \pi }{3} \)であることがわかります。
つまり
\[ \frac{ \sqrt{3} }{2} \cos x + \frac{1}{2} \sin x = \sin (x + \frac{ \pi }{3} ) \]
以上より、
\begin{align*}
&y = \sqrt{3} \cos x + \sin x \\
\Leftrightarrow \ &y = 2 \sin (x + \frac{ \pi }{3} )
\end{align*}
となります。
その他の公式
教科書や参考書、問題集を見ていると、以下のような公式がたくさん記載されています。
しかし、暗記しなくても構いません。三角比の定義を考えればわかりますし、最悪、加法定理を用いれば導けるからです。
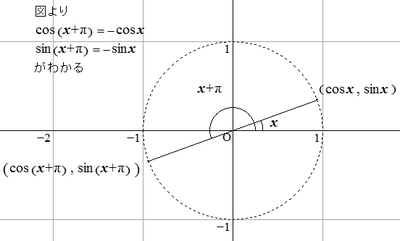
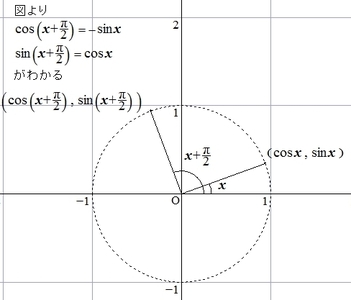
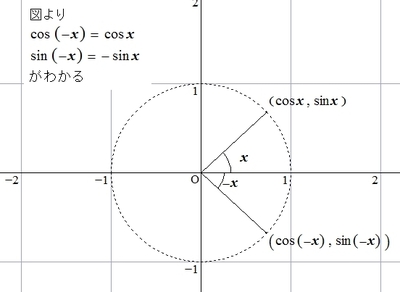
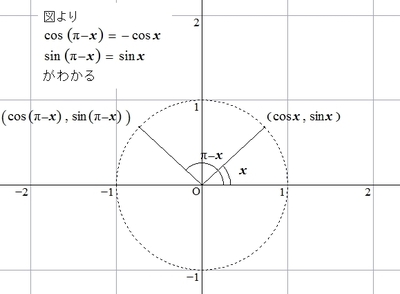
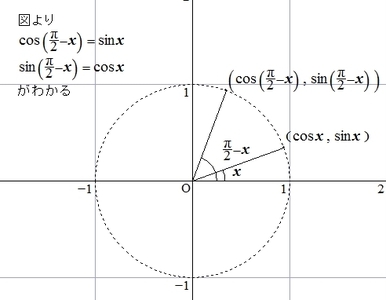
以下では、三角比の定義からそれぞれの公式が成り立つことを見ていきます。
(1)
\( 2 \pi \)回転すると、ちょうど１回転し、同じ場所に戻るため、(1)の公式が成り立ちます。
(2)
以下のグラフより公式が成り立つことが確認できる。
(3)
以下のグラフより公式が成り立つことが確認できる。
(4)
以下のグラフより公式が成り立つことが確認できる。
(5)
以下のグラフより公式が成り立つことが確認できる。
(6)
以下のグラフより公式が成り立つことが確認できる。
