数列とは、”ある規則に従って並べられた数”のこと。
たとえば
\begin{align*}
& 2,5,8,11,14,\cdots \\
& 3,6,12,24,48,\cdots \\
& 1,2,4,7,11,16,\cdots
\end{align*}
など。
こういった数が
- どういった規則に従って並べられたのか?
- どのような形で表されるのか?
ということを考えていくのが数列という分野です。
なので

教科書に公式として載っているから、とりあえず丸暗記しておこう
とするのではなく、

この公式は、どのように導かれたのだろう?
と考えることが大事になってきます。
数列という分野では、難しい問題になればなるほど
- 規則性を考える
- 具体的な場合を考える
といった発想法が重要になります。
そういった発想法に慣れるために、まずは簡単な規則から作られる
- 等差数列
- 等比数列
といった数列から練習していきましょう。
ここでは
\begin{align*}
2,5,8,11,14,\cdots
\end{align*}
といったような、一定の数を足して作った”等差数列”を考えていきます。
【数列の表し方などについて】
数列では、
1番目の数を\( a_{1} \)
2番目の数を\( a_{2} \)
3番目の数を\( a_{3} \)
…
n番目の数を\( a_{n} \)
といった文字を使って表すことが一般的です。
そして
1番目の数を初項
2番目の数を第2項
3番目の数を第3項
…
n番目の数を第n項
という言い方をします。
ここでも、そのような表し方・言い方をしています。
等差数列の一般項の公式は、簡単に導き出せる
等差数列とは
ある数に、次々と一定数を足していく
という規則に従って作られた数列のことをいいます。(次々に足していく数のことを”公差”といいます。)
言い換えれば
ひとつ前の数に一定数を加えて作った数列
とも言えます。
たとえば、冒頭であげた
\begin{align*}
2,5,8,11,14,\cdots
\end{align*}
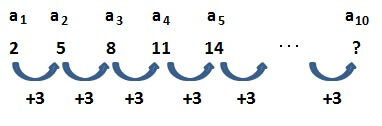
は、最初の数\( 2 \)に、公差\( 3 \)を次々と足して作った数列です。
さて、この数列の10番目の数はいくつになるでしょうか?
この数列の関係性を表した以下の図を見ながら考えていきましょう。
この図から考えていただきたいのは
\( a_1 \)との関係性
について。
\( a_2 \)、\( a_3 \)、\( a_4 \)、\( a_5 \)は、それぞれ\( a_1 \)に\( 3 \)を何回足した数でしょうか。
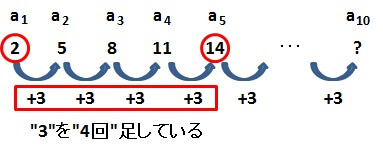
図からわかるように
\( a_2 \)は、\( a_1 \)に\( 3 \)を1回足した数
\( a_3 \)は、\( a_1 \)に\( 3 \)を2回足した数
\( a_4 \)は、\( a_1 \)に\( 3 \)を3回足した数
\( a_5 \)は、\( a_1 \)に\( 3 \)を4回足した数
になっています。(下の図は、\( a_5 \)について強調したものです。)
それぞれの関係を、式で表せば次のようになります。
\begin{align*}
& a_2 = a_1 + 3 \cdot 1 \\
& a_3 = a_1 + 3 \cdot 2 \\
& a_4 = a_1 + 3 \cdot 3 \\
& a_5 = a_1 + 3 \cdot 4 \\
\end{align*}
同じように考えていくと
\( a_{10} \)は、\( a_{1} \)に\( 3 \)を9回足した数
になることがわかります。
つまり
\begin{align*}
a_{10} & = a_1 + 3 \cdot 9 \\
& = 2 + 27 \\
& = 29
\end{align*}
と求めることができます。
では、n番目の数はどのように表すことができるでしょうか。
10番目の数の場合と同じように
\( a_2 \)は、\( a_1 \)に\( 3 \)を1回足した数
\( a_3 \)は、\( a_1 \)に\( 3 \)を2回足した数
\( a_4 \)は、\( a_1 \)に\( 3 \)を3回足した数
\( a_5 \)は、\( a_1 \)に\( 3 \)を4回足した数
…
\( a_{10} \)は、\( a_1 \)に\( 3 \)を9回足した数
…
と考えていくと、
\( a_n \)は、\( a_1 \)に\( 3 \)をn-1回足した数
であることがわかります。
つまり、初項が\( 2 \)、公差\( 3 \)の数列\( \{ a_n \} \)の一般項\( a_n \)は
\begin{align*}
a_n & = 2 + 3(n – 1) \\
& = 3n – 1
\end{align*}
と表すことができるのです。
ここまでの復習も兼ねて、初項\( a_1 \)、公差\( d \)の等差数列の一般項\( a_n \)を考えてみましょう。
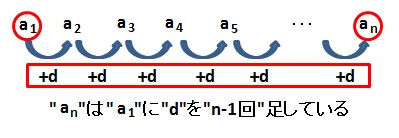
ここまで見てきたように考えれば、
\( a_n \)は、初項\( a_1 \)に公差\( d \)をn-1回足した数
といえます。
これを式にすると
\[ a_{n} = a_1 + d(n-1) \]
となるのです。
初項\( a_1 \)、公差\( d \)の等差数列\( \{ a_n \} \)の一般項\( a_n \)は、
\begin{align*}
a_n = a_1 + (n-1)d \\
\end{align*}
と表すことができる。
等差数列の問題を解くときは、この公式にただ当てはめるのではなく、ここまで見てきた”\( a_n \)と\( a_1 \)との関係性”を意識して解くことが大事です。
等差数列の和の公式のポイントは、”もうひとつを逆から並べて足す”
1からnまでの和を求める
まずは、いちばん簡単な等差数列
\[ 1,2,3,\cdots ,n \]
の和を求めてみましょう。
※長くなったので、ページを分けました。
リンク:数を逆からもうひとつ並べて、自然数の和を求める方法

そして、この考え方をすれば、1からnまでの和だけでなく、一般的な等差数列の初項から第n項までの和を求めることができるのです。
等差数列の初項から第n項までの和を求める
まずは、具体的な数列で等差数列の和の求め方を見ていきましょう。
例として、等差数列の一般項を求めるところでも使った
\begin{align*}
2,5,8,11,14,\cdots
\end{align*}
という初項が\( 2 \)で公差\( 3 \)の数列を考えます。
この数列の初項から第10項までの和はいくらでしょうか。(ちなみに、一般項の説明で見たように、第10項は”29″です。)
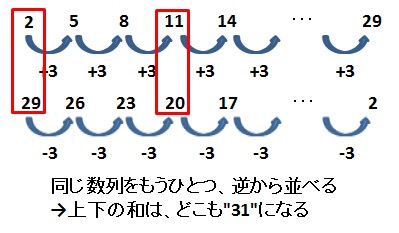
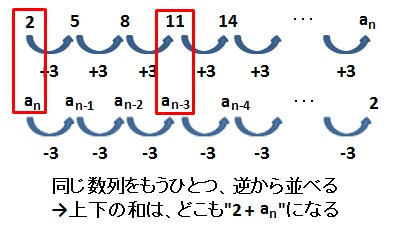
1から11までの和を求めたのと同じように、逆順にした数列を元の数列の下に並べます。
そうすると、初項と第10項(最後の項)の和”31″が10個出来上がります。
(右に行くにつれて、上の数列は”+3″されていきますが、下の数列は”-3″されていきますので、上下の和はどこも等しくなります。)
図には、和を求めたい数列が2回出てきていますので
\[ 31 \times 10 \times \frac{1}{2} = 155 \]
と計算できるということです。
では、初項から第n項までの和はどうなるでしょうか。
これまでと同じように、初項から第n項までの和を上下に並べてみます。
そうすると、初項から第10項までの和を求めたときと同じように考えると、初項と第n項(最後の項)の和”\( 2 + a_{n} \)”がn個できることがわかります。
図には、和を求めたい数列が2回出てきていますので、2で割って
\[ \frac{1}{2} n (2 + a_{n}) \]
となります。
また、等差数列の一般項を求めるところで計算したように、初項が\( 2 \)、公差\( 3 \)の数列は
\[ a_{n} = 3n – 1 \]
であったので、この数列の和は
\[ \frac{1}{2} n (2 + 3n – 1 ) = \frac{1}{2} n (3n + 1 ) \]
と表すこともできます。
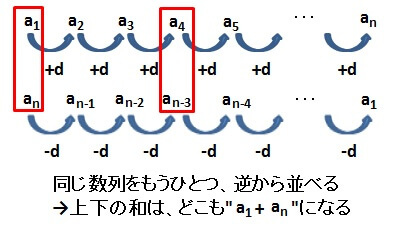
最後に復習も兼ねて、初項\( a_1 \)、公差\( d \)の等差数列の初項から第n項までの和を考えてみましょう。
これまでと同じように、初項と第n項の和”\( a_1+ a_{n} \)”がn個できることがわかります。
図には、和を求めたい数列を2個並べたので、求めたい和は
\[ \frac{1}{2} n( a_1+ a_{n} ) \]
と表すことができます。
ちなみに、初項\( a_1 \)、公差\( d \)の等差数列\( \{ a_n \} \)は
\begin{align*}
a_n = a_1 + (n-1)d \\
\end{align*}
と表すことができるので、和の公式は
\begin{align*}
& \frac{1}{2} n( a_1+ a_1 + (n-1)d ) \\
= & \frac{1}{2} n( 2a_1 + (n-1)d )
\end{align*}
とも表すことができるのです。
初項\( a_1 \)、公差\( d \)の等差数列\( \{ a_n \} \)の初項から第n項までの和は
\[ \frac{1}{2} n( a_1+ a_{n} ) \]
または
\[ \frac{1}{2} n( 2a_1 + (n-1)d ) \]
と表すことができる。
一般項の公式と同じように、この公式もただ丸暗記してはいけません。
“和を求めたい数列をもうひとつ逆順に並べると、上下の和はどれも\( a_1+ a_{n} \)になる”という構造を意識して導き出せるようにしておくことが大切になります。