ユークリッドの互除法をはじめて学習したとき
「なぜ、ユークリッドの互除法を使うと最大公約数が求められるのか、原理がわからない…」
「ユークリッドの互除法の証明を見ても、いまいちピンとこない…」
と思われる方は多いのではないでしょうか。
ここでは
”なぜ、ユークリッドの互除法が成り立つのか”
を、図で見て理解できるように説明いたします。
そして、ユークリッドの互除法を応用する上でポイントとなる
”都合の良い部分とそうでない部分に分ける”
という考え方を見ていきましょう。
これは、他のところでも使える考え方なので、ぜひ理解してみてください。
ユークリッドの互除法とは? 最大公約数を求めるやり方
まず最初に、ユークリッドの互除法を知らない方や忘れてしまった方のために、”ユークリッドの互除法とは、どういうものか?”ということから始めましょう。
2つの自然数\( a \)、\( b \)に対して、\( a \) を\( b \)で割ったときの余りを\( r \)とする。
このとき「\( a \) と\( b \)の最大公約数」は「\( b \) と余り\( r \)の最大公約数」に等しくなる。
例として、\( 56 \) と \( 36 \) の最大公約数を考えてみましょう。
\( 56 \) を \( 36 \) を割ると
\[ 56 \ \div \ 36 = 1 \cdots 20 \]
となるので
\( 56 \) と \( 36 \) の最大公約数は、\( 36 \) と \( 20 \) の最大公約数と同じである
ということをユークリッドの互除法は言っているのです。
そして、実際に最大公約数を求める場合は、割った数\( 36 \) と余りの \( 20 \) に対しても
\[ 36 \ \div \ 20 = 1 \cdots 16 \]
というふうに、割り算を行います。
このように割り算を繰り返していくことで、数がどんどんと小さくなっていき、最終的に最大公約数を見つけられる、ということです。
つまり、\( 56 \) と \( 36 \) の最大公約数は、ユークリッドの互除法を使うと
\begin{align*}
& 56 \ \div \ 36 = 1 \cdots 20 \\
& 36 \ \div \ 20 = 1 \cdots 16 \\
& 20 \ \div \ 16 = 1 \cdots \phantom{0} 4 \\
& 16 \ \div \ \phantom{0} \underline{4} = 4
\end{align*}
と割り算を繰り返すことで、\( 56 \) と \( 36 \) の最大公約数は \( 4 \) である、と求めることができるのです。
図で見ると、ユークリッドの互除法の仕組みや原理がわかる
では、なぜユークリッドの互除法が成り立ち、最大公約数が求められるのでしょうか。
それを理解するために、次のようなタイル貼りの問題を考えていきます。
(問題)
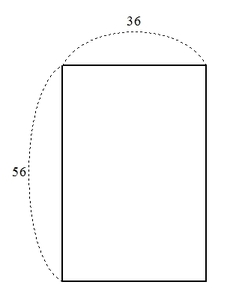
縦\( 56 \)、横 \( 36 \) の長方形の敷地がある。いま、この敷地に正方形のタイルで隙間なく敷き詰めたい。隙間なく敷き詰められるタイルのうち、1辺の長さが最大のタイルを求めよ。
ただし、正方形の1辺の長さは自然数とする。
(解説)
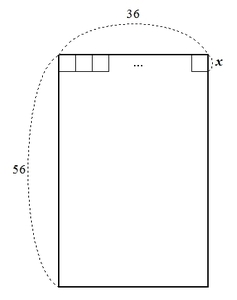
縦\( 56 \)、横 \( 36 \) の長方形の敷地に対して、1辺が\( x \)の正方形のタイルで隙間なく敷き詰められると仮定します。
まず、1辺の長さが\( x \)のタイルを横に敷き詰めていきましょう。
すると、以下の図のように、横幅にピッタリと収まります。
このように、端まで敷き詰めたとき、タイルを\( n \)枚使ったとすると
\[ 36 = x \times n \]
が成り立ちますので、\( x \)は\( 36 \)の約数であるということがいえます。
また、縦についても、同様に考えると\( x \)は\( 56 \)の約数であることがわかります。
さらに、2列目、3列目…とタイルを敷き詰めていきましょう。
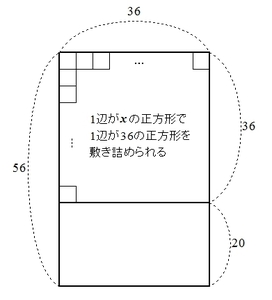
すると、以下の図のように、1辺が\( 36 \)の正方形の敷地を、1辺が\( x \)のタイルで隙間なく敷き詰められることがわかります。
いま、1辺\( x \)のタイルで縦\( 56 \)、横 \( 36 \) の敷地が敷き詰められると仮定したので、まだタイルが敷き詰められていない縦 \( 20 \)、横 \( 36\) の長方形も1辺\( x \)のタイルで隙間なく敷き詰められなくてはなりません。
つまり
「1辺\( x \)の正方形で、縦\( 56 \)、横\( 36 \)の長方形が隙間なく敷き詰められる」ならば「1辺\( x \)の正方形で、縦\( 20 \)、横\( 36 \)の長方形が隙間なく敷き詰められる」
ということが言えます。
さらに、縦\( 20 \)、横\( 36 \)の長方形についても、タイルを敷き詰めていきましょう。
すると、以下の図のように、1辺が\( x \)の正方形で1辺が\( 20 \) の正方形を敷き詰めることができることがわかります。
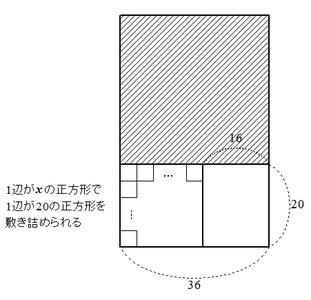
このことから、\( x \)は\( 20 \)の約数でもあることがわかります。
さらに、残りの縦\( 20 \)、横\( 16 \)の長方形も1辺\( x \)の正方形で隙間なく敷き詰められなければなりません。
つまり
「1辺\( x \)の正方形で、縦\( 20 \)、横\( 36 \)の長方形が隙間なく敷き詰められる」ならば「1辺\( x \)の正方形で、縦\( 20 \)、横\( 16 \)の長方形が隙間なく敷き詰められる」
ということになります。
さらに、これまでやってきたようにタイルを敷き詰めていくことで、以下のような図を得ることができます。
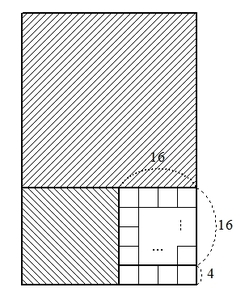
つまり
「1辺\( x \)の正方形で、縦\( 20 \)、横\( 16 \)の長方形が隙間なく敷き詰められる」ならば「1辺\( x \)の正方形で、縦\( 4 \)、横\( 16 \)の長方形が隙間なく敷き詰められる」
ということになります。
このことから、\( x \)は\( 16 \)の約数でもあることがわかります。
さらに、縦\( 4 \)、横 \( 16 \) の長方形は1辺が \( 4 \) の正方形で敷き詰めることができます。
また、1辺が\( 5 \) 以上の正方形では、縦\( 4 \)、横 \( 16 \) の長方形からはみ出します。
よって、縦 \( 4 \)、横 \( 16 \) の長方形を敷き詰めることができる正方形のうち、最も大きいのは1辺が \( 4 \) の正方形となります。
つまり、\( 4 \) は、\( 16 \) の最大公約数であることがわかります。
ここまでの流れをまとめると、以下のようになります。
\( x \)は、\( 56 \)と\( 36 \)の公約数である
\( \Rightarrow \)\( x \)は、\( 20 \)の約数でなければならない
\( \Rightarrow \)\( x \)は、\( 16 \)の約数でなければならない
\( \Rightarrow \)\( x \)は、\( 4 \)の約数でなければならない
\( \Rightarrow \)\( 16 \)と\( 4 \)の公約数のうち、最大なのは \( 4 \)
つまり
\( 56 \)と\( 36 \)の最大公約数は、\( 4 \) である
ということが言えるのです。
ユークリッドの互除法のポイントは、”都合のいい部分とそうでない部分を分ける”こと
ユークリッドの互除法を図で見ることで、その原理や仕組みが理解できたでしょうか。
ここでは、復習の意味も込めて、いままで図で見てきたことを数字の世界でも見ていきましょう。
ポイントとなるのは
”都合のいい部分とそうでない部分を分ける”
ということです。
まず、\( x \)が\( 56 \) と \( 36 \) の公約数であるとします。つまり、\( 56 \) も \( 36 \) も\( x \)で割り切れることになります。
また、\( 56 \) は
\[ 56 = 36 + 20 \]
というように\( 36 \) と \( 20 \) に分けることができます。
そうすることによって
\( 56 \) と \( 36 \) が\( x \)で割り切れるので、\( 20 \) も\( x \)で割り切れないと矛盾が生じる
ということがわかります。
つまり
\( x \) で割り切れる”都合のいい部分”と”そうでない部分”に分けてみたら、実はそうでない部分も\( x \) で割り切れなければならない
ということがわかったのです。
さらに、\( 36 \)についても同じように
\[ 36 = 20 + 16 \]
と分けることができますので、\( 16 \) も\( x \)で割り切れなければならない。
\( 20 \)も同様に
\[ 20 = 16 + 4 \]
とでき、\( 16 \) も\( x \)で割り切れなければならない。
また、ここまで来ると、数字も小さくなり、\( 16 \) と\( 4 \) の最大公約数は \( 4 \) であることが簡単にわかります。
つまり、ここでも
\( x \)は、\( 56 \)と\( 36 \)の公約数である
\( \Rightarrow \)\( x \)は、\( 20 \)の約数でなければならない
\( \Rightarrow \)\( x \)は、\( 16 \)の約数でなければならない
\( \Rightarrow \)\( x \)は、\( 4 \)の約数でなければならない
\( \Rightarrow \)\( 16 \)と\( 4 \)の公約数のうち、最大なのは \( 4 \)
となります。
つまり
\( 56 \)と\( 36 \)の最大公約数は\( 4 \) である
とわかります。
この考え方を使うと、”不定方程式を解く際に、なぜユークリッドの互除法を使うのか?”ということがわかります。
※詳細については、不定方程式で詳しく紹介していますので、合わせてご覧いただけると理解が深まります。