”平方完成”さえできれば、2次方程式や2次関数の問題はほとんど解くことができます。
なぜなら、”平方完成”ができれば、2次関数の頂点(最大値・最小値)や対称の軸、\( x \)軸との交点など、グラフを描く上で必要となる情報がすべてわかるからです。
ここでは、
- 2次関数の頂点(最大値・最小値)や対称の軸、\( x \)軸との交点
- 実際に平方完成を使った問題の解き方
について説明いたします。
平方完成ができれば、グラフが描ける
平方完成とは、” \( ax^2 + bx + c \) を \( a(x + p )^2 + q \) という形にすることである”と、”平方完成”の意味や手順・やり方についてで見ました。
2次関数において、平方完成することでわかることは、次の3つです。
- グラフの概形
- 頂点の座標・対称の軸
- \( x \)軸との交点
それぞれひとつずつ見ていきましょう。
グラフの概形は、\( x^2 \)の係数\( a \)によって変わる
まずは、2次関数のグラフの概形についてです。
2次関数のグラフの概形は、\( x^2 \) の係数 \( a \) の正負によって変わります。
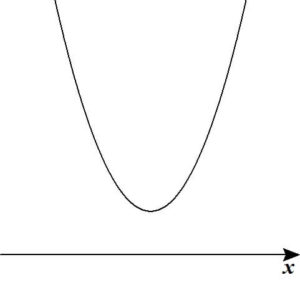
- \( x^2 \) の係数が正の場合:下に凸のグラフ(図1)
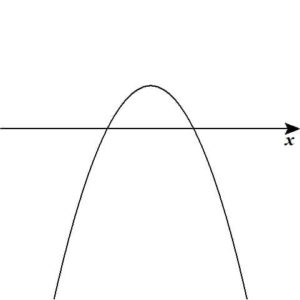
- \( x^2 \) の係数が負の場合:上に凸のグラフ(図2)
となります。
【図1:”下に凸”のグラフ】
こういったグラフになる理由は、平方完成した形
\[ y = a(x + p )^2 + q \]
を見ていくと理解できます。
変数\( x \)によって変化するのは、\( a(x + p )^2 \)の部分です。
そして、実数は2乗すると、\( 0 \)以上になるので、
\[ (x + p )^2 \geq 0 \]
となります。
つまり
\( a > 0 \)の場合
\[ a(x + p )^2 \geq 0 \]
\( a < 0 \)の場合
\[ a(x + p )^2 \leq 0 \]
ということがわかります。
これは、言い換えると
\( a > 0 \) の場合、\( x \) の値が \( – p \)から離れるほど \( y \) の値は大きくなる
\( a < 0 \) の場合、\( x \) の値が \( – p \)から離れるほど \( y \) の値は小さくなる
ということです。
そして、その様子をグラフに表すと、図1や図2のようになる、ということです。
2次関数のグラフは、\( x^2 \)の係数\( a \)の正負によって形が変わる
- \( x^2 \)の係数が正の場合:下に凸のグラフ
- \( x^2 \)の係数が負の場合:上に凸のグラフ
頂点の座標は、平方完成をすればわかる
次に説明するのは、最大値・最小値(グラフの頂点)について、です。
ここでも、平方完成した形
\[ y = a(x + p )^2 + q \]
を見ていきます。
\( a > 0 \) の場合
\[ a(x + p )^2 \geq 0 \]
となるのは、すでに見てきたとおりです。
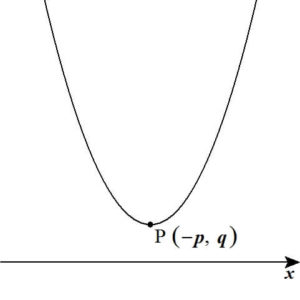
つまり、\( x = – p \) のとき、\( a(x + p )^2 = 0 \) となるので \( y \) は最小値 \( q \) をとります。(図3)
同様に、\( a < 0 \) の場合
\[ a(x + p )^2 \leq 0 \]
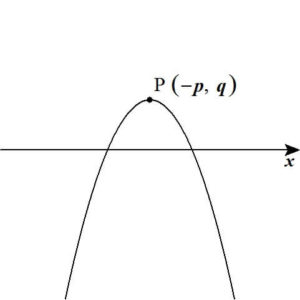
であるので、\( x = – p \) のとき、\( y \) は最大値 \( q \) をとることがわかります。(図4)
【図3:”下に凸”のグラフの頂点】
【図4:”上に凸”のグラフの頂点】
\( y = ax^2 + bx + c \) が \( y = a(x + p )^2 + q \) と変形できたとき、頂点の座標は \( ( – p ,q) \) となる。
さらに
- \( a > 0 \) なら、定数項の\( q \) は\( y \)の最小値
- \( a < 0 \) なら、定数項の\( q \) は\( y \)の最大値
となる。
実数解の個数(\( x \)軸との共有点の個数)は、\( x^2 \)の係数と頂点の座標を見ればわかる
最後に、実数解の個数(\( x \)軸との共有点の個数)についての説明です。
ここまで、\( a > 0\)のとき
- 下に凸のグラフ
- 頂点の\( y \)座標の値が、2次関数の最小値になる
ということを見てきました。
この2つのことから
- 頂点の\( y \)座標が\( 0 \)より大きければ、\( x \)軸との共有点を持たない
- 頂点の\( y \)座標が\( 0 \)となれば、\( x \)軸との共有点を1つ持つ
- 頂点の\( y \)座標が\( 0 \)より小さければ、\( x \)軸との共有点を2つ持つ
ということがわかります。(図5)
同様に、\( a < 0\)のとき
- 上に凸のグラフ
- 頂点の\( y \)座標の値が、2次関数の最大値になる
ということを見てきました。
この2つのことから
- 頂点の\( y \)座標が\( 0 \)より大きければ、\( x \)軸との共有点を2つ持つ
- 頂点の\( y \)座標が\( 0 \)であれば、\( x \)軸との共有点を1つ持つ
- 頂点の\( y \)座標が\( 0 \)より小さければ、\( x \)軸との共有点を持たない
ということがわかります。(図6)
【図5:下に凸のグラフで、\( x \)軸との共有点を持たない例】
【図6:上に凸のグラフで、\( x \)軸との共有点を2つ持つ例】
\( a > 0\)のとき
- 頂点の\( y \)座標が\( 0 \)より大きければ、\( x \)軸との共有点を持たない
- 頂点の\( y \)座標が\( 0 \)となれば、\( x \)軸との共有点を1つ持つ
- 頂点の\( y \)座標が\( 0 \)より小さければ、\( x \)軸との共有点を2つ持つ
\( a < 0\)のとき
- 頂点の\( y \)座標が\( 0 \)より大きければ、\( x \)軸との共有点を2つ持つ
- 頂点の\( y \)座標が\( 0 \)であれば、\( x \)軸との共有点を1つ持つ
- 頂点の\( y \)座標が\( 0 \)より小さければ、\( x \)軸との共有点を持たない
平方完成を使って2次関数の問題を解いてみる
ここでは、代表的な問題をいくつか解いていきたいと思います。
どの問題でも、まずは”平方完成をして、グラフの概形を把握すること”からはじめてください。
どの問題も、基本的には
- 平方完成する
- グラフの概形を書く
という手順で始めます。
問題1:判別式を使わなくても、問題は解ける
参考書などでは「判別式より…」という解説がなされている問題があります。
しかし、ただ判別式を当てはめて解いているだけでは正しい理解に結びつきません。
そういった問題でも、平方完成を使えば解けますし、理解も深まっていきます。
(問題1)
2次関数 \( y = x^2 + 2ax + (a + 2) \) のグラフが\( x \)軸と共有点をもたないとき、実数\( a \)の値はどのような範囲にあるか。
(解説)
まず、「2次関数\( y = x^2 + 2ax + (a + 2) \)のグラフが\( x \)軸と共有点をもたない」とはどういった状態のことでしょうか?
いままでの解説で見てきたように、\( x \)軸との共有点を考える上で大切なことは
- \( x^2 \)の係数(グラフの概形)
- 頂点の座標
の2つです。
まず、\( x^2 \)の係数を見ていきましょう。
いま考えている2次関数\( y = x^2 + 2ax + (a + 2) \)は、\( x^2 \)の係数が \( 1 \) 。
なので、”下に凸”のグラフになります。
つまり、頂点の\( y \)座標が\( 0 \)より大きければ、\( x \)軸との共有点を持たないということです。
次に、頂点の\( y \)座標の値を求めていきましょう。
頂点の\( y \)座標の値は、\( y = a(x + p)^2 + q \)と平方完成したときの定数項\( q \)にあたる部分の値です。
なので、いま考えている2次関数\( y = x^2 + 2ax + (a + 2) \)を平方完成していきましょう。
\begin{align*}
y &= x^2 + 2ax + (a + 2) \\
&= (x^2 + 2ax + a^2 – a^2) + (a + 2) \\
& = (x + a)^2 – a^2 + (a + 2) \\
& = (x + a)^2 – (a^2 – a – 2) \\
& = (x + a)^2 – (a – 2)(a + 1)
\end{align*}
したがって、頂点の\( y \)座標は\( – (a – 2)(a + 1) \)です。
この\( – (a – 2)(a + 1) \)が\( 0 \)より大きければ共有点を持ちません。
よって、共有点をもたない条件は
\begin{align*}
& – (a – 2)(a + 1) > 0 \\
\Leftrightarrow \ & (a – 2)(a + 1) < 0 \\
\Leftrightarrow \ & -1 < a < 2
\end{align*}
であるということがわかります。
問題2:最大値・最小値の問題は平方完成できないと解けない
2次関数の最大値・最小値を求める問題は、頂点の \( y \) 座標を求められないと解くことができません。
しかし、その頂点の座標は、解の公式や判別式では求めることはできません。平方完成ができないと、求めることはできないのです。
(問題2)
\( 0 \le x \le 2 \)の範囲において、2次関数\( f(x) = x^2 – 2ax + a \)の最小値・最大値を求めよ。
(解説)
問題を考えるうえで、まずはグラフの概形を把握しましょう。
\( x^2 \)の係数は、\( 1 \)なので、下に凸のグラフを描きます。
次に、\( f(x) = x^2 – 2ax + a \)を平方完成して頂点の座標を求めていきましょう。
\begin{align*}
f(x) &= x^2 – 2ax + a \\
&= (x^2 – 2ax + a^2) – a^2 + a \\
&= ( x – a )^2 – a^2 + a
\end{align*}
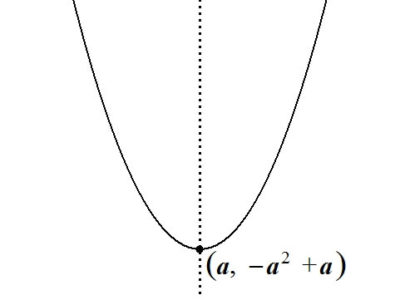
となり、頂点の座標が\( (a,- a^2 + a) \)であることがわかります。
よって、グラフの概形は以下のようになります。
次に考えるのは、「グラフの軸\( x = a \)が、\( 0 \le x \le 2 \)に対して、どの位置にあるのか?」ということです。
その様子は、次のように\( x \)の範囲を動かしてみるとよくわかります。
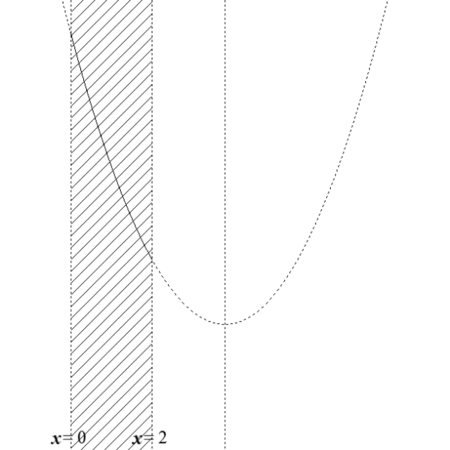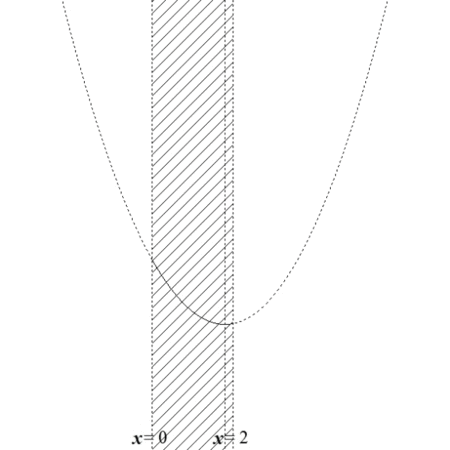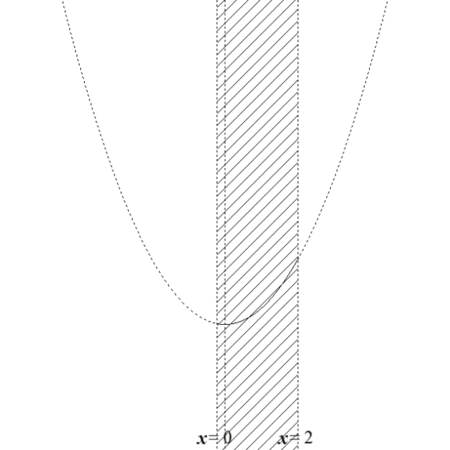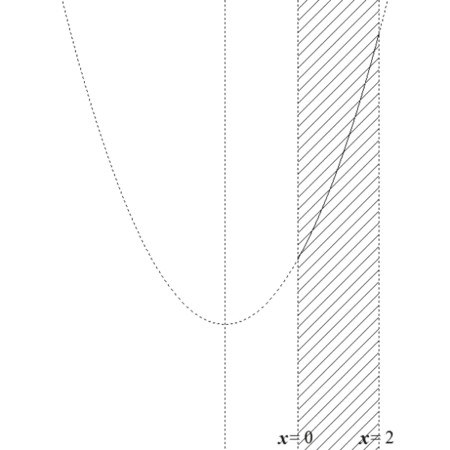
【図7:\( x \)の範囲を動かした図】
図7の様子から、最小値に関して、以下の3通りが考えられます。
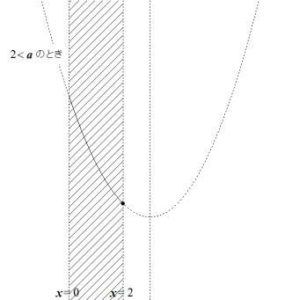
- 軸\( x = a \)が\( 0 \le x \le 2 \)より右にあるとき、最小値は\( f(2) \)
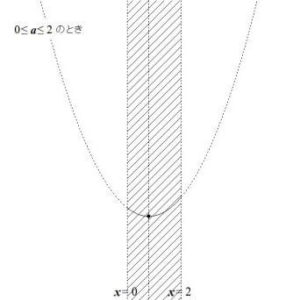
- 軸\( x = a \)が\( 0 \le x \le 2 \)の範囲にあるとき、最小値は\( f(a) \)
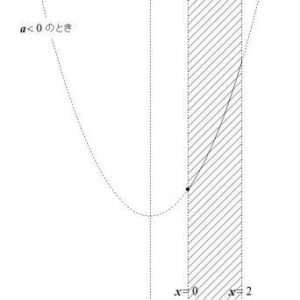
- 軸\( x = a \)が\( 0 \le x \le 2 \)より左にあるとき、最小値は\( f(0) \)
以上より
- \( 2 < a \)のとき、最小値は\( f(2) = 4 – 3a \)
- \( 0 \le a \le 2 \)のとき、最小値は\( f(a) = -a^2 + a \)
- \( a < 0 \)のとき、最小値は\( f(0) = a \)
ということがわかります。
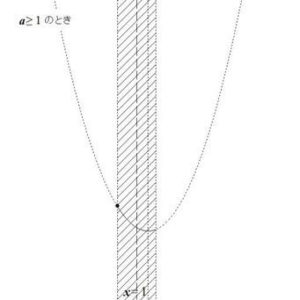
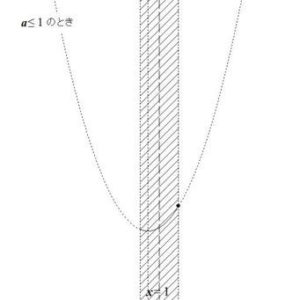
最大値についても、最小値の場合と同様に考えていきます。
図7の様子より、最大値については、以下の2通りが考えられます。
以上より
- \( a \ge 1 \)のとき、最小値は\( f(0) = a \)
- \( a \le 1 \)のとき、最小値は\( f(1) = 4 – 3a \)
となります。