”合同・相似”を深く知れば、三角比や正弦定理・余弦定理の理解も深くなるで、”三角形の辺や角の大きさといった条件をいくつか与えると、その条件をみたす三角形がただひとつに決まる”と説明いたしました。
そこで、次のような疑問を感じた方はいませんか?
「じゃあ、与えられた以外の辺の長さや角の大きさって、求められないのか?」
それは、高校の数学で学ぶ”正弦定理・余弦定理”を使えば可能になります。
ここで紹介する”三角比”は、その”正弦定理・余弦定理”を理解するために必要な知識です。
まずは、”三角比”がどのような発想で生み出されたのかを見ていくことで理解を深めていきましょう。
ここでは、
- 合同・相似の発想から三角比へ
- 三角比の2つの定義(「直角三角を用いた定義」と「単位円を用いた拡張された定義」
- \( 30^\circ \)、\( 45^\circ \)、\( 60^\circ \)の三角比の求め方
- 三角比の相互関係を表す公式の導き方
について説明いたします。
直角三角形の鋭角が与えられれば、各辺の比がわかる
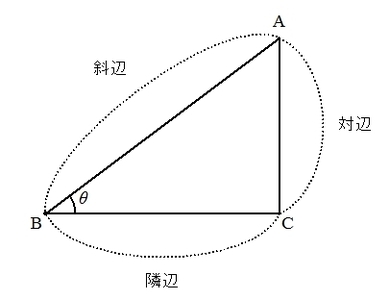
まず、三角比を学ぶ上で必要になる言葉の説明からはじめます。
以下の図のように、直角三角形のひとつの鋭角が\( \theta \)と与えられたとき
- 直角と隣接していない辺を斜辺
- 鋭角 \( \theta \) と隣接している辺を隣辺
- 鋭角 \( \theta \) と隣接していない辺を対辺
といいます。
ここから本題である”三角比”の説明に入っていきます。
”合同・相似”を深く知れば、三角比や正弦定理・余弦定理の理解も深くなるでも見たように、角度が2つ与えられれば、三角形の形はただひとつに決まります。
つまり、直角三角形では、直角以外の角度がひとつ与えられれば、三角形の形はただひとつに決まります。
そこで、直角三角形のひとつの鋭角が与えられたとき、あらかじめ各辺の比がわかっていれば便利ではありませんか?
各辺の比がわかっていれば、直角三角形の辺の長さがひとつでも与えられれば、他の辺の長さも計算することができます。
例えば、\( \angle ACB = 90^\circ, \angle ABC = 54^\circ, AB = 1 \)の直角三角形\( ABC \)を考えます。
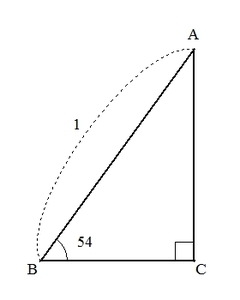
もし、各辺の比がわかっていれば、条件として与えられた辺\( AB \)以外の辺\( AC,BC \)の長さを求めることができます。
実際、\( \angle ABC = 54^\circ \)のとき、各辺の比は
\begin{align*}
AB : BC = 1 : 0.5878… \\
AB : AC = 1 : 0.8090…
\end{align*}
となります。
つまり、\( AB = 1 \)なら
\begin{align*}
BC = 0.5878… \\
AC = 0.8090…
\end{align*}
と求めることができるのです。
合同・相似の発想から三角比の定義へ
ここまで見てきたように、直角三角形では、直角以外の角がわかれば各辺の比がただ1通りに決まります。
数学では、以下のように、各辺の比を\( \sin \)、\( \cos \)、\( \tan \)という記号を使って、分数の形で表します。
【三角比の定義(直角三角形を用いた定義)】
直角三角形\( ABC \)において、\( AB = r \)、\( BC = x \)、\( AC = y \)、\( \angle ABC = \theta \)としたとき、\( \sin \theta \)、\( \cos \theta \)、\( \tan \theta \)はそれぞれ
\begin{align*}
\sin \theta = \frac{y}{r} \\
\cos \theta = \frac{x}{r} \\
\tan \theta = \frac{y}{x}
\end{align*}
と表す。(ただし、\( 0^\circ < \theta < 90^\circ \))
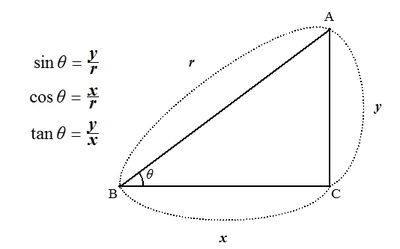
簡単に言えば、三角比とは、直角三角形の各辺の比を表したものなのです。

ん?なんかピンとこないな…
なんてお思いの方は、\( \sin \)、\( \cos \)の定義を、次のように言い換えた形を見ていただければ、イメージしやすいのではないでしょうか。
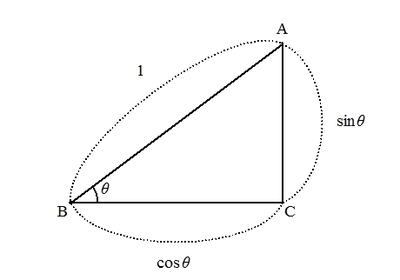
三角比の定義は、次のように言い換えることができる。
斜辺の長さが\( r \)のとき
- 隣辺の長さが \( r\sin \theta \)
- 対辺の長さが \( r\cos \theta \)
になる。
特に、斜辺の長さが1なら
- 隣辺の長さが\( \sin \theta \)
- 対辺の長さが\( \cos \theta \)
になる。
また、
- 三角形の勾配(傾き)が\( \tan \theta \)
正n角形から導かれる3つの三角比 ※”覚え方”なんてもういらない
直角三角形では、”直角以外の角が与えられれば各辺の比がただ1通りに定まる”とここまで述べてきました。

でも、そもそも各辺の比って求められるの?
残念ながら、いまの段階では限られた三角比しか求めることはできません。
しかし、学習が進んでいくことで、数多くの三角比が求められるようになっていきます。
いまの段階では、正n角形を利用することで三角比の値を求めることができるものがあります。
特に、正三角形・正方形を使って求められる\( 30^\circ \)、\( 45^\circ \)、\( 60^\circ \)の三角比は重要になってきますので、しっかりと理解していきましょう。
※それぞれの値を暗記しようとするのではなく、必要なときに、これから紹介する方法で導き出せるようにしておきましょう。
正三角形から導かれる\( 30^\circ \)、\( 60^\circ \)の三角比
まずは、1辺の長さが1である正三角形を利用することで、\( 30^\circ \)、\( 60^\circ \)の三角比を求めることができます。
以下の図のように、頂点Aから辺BCに垂線を引き、垂線との交点をDとします。
このとき、点Dは辺BCの中点となるので
\[ BD = \frac{1}{2} \]
となります。
そして、辺ADは、三平方の定理(ピタゴラスの定理)を使うことで
\begin{align*}
AB^2 &= AD^2 + BD^2 \\
\Rightarrow \ AD^2 &= 1- (\frac{1}{2})^2 \\
\Rightarrow \ AD &= \frac{ \sqrt{3} }{2}
\end{align*}
となります。
この図から
\begin{cases}
\begin{align*}
\sin 60^\circ & = \frac{AD}{AB} = \frac{ \sqrt{3} }{2} \\
\cos 60^\circ & = \frac{BD}{AB} = \frac{1}{2} \\
\tan 60^\circ & = \frac{AD}{BD} = \sqrt{3}
\end{align*}
\end{cases}
\begin{cases}
\begin{align*}
\sin 30^\circ & = \frac{BD}{AB} = \frac{1}{2} \\
\cos 30^\circ & = \frac{AD}{AB} =\frac{ \sqrt{3} }{2} \\
\tan 30^\circ & = \frac{BD}{AD} =\frac{1}{ \sqrt{3} }
\end{align*}
\end{cases}
であることがわかります。
正方形から導かれる\( 45^\circ \)の三角比
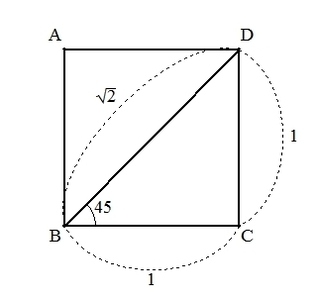
次に、1辺の長さが1である正方形を利用して、\( 45^\circ \)の三角比を求めていきます。
以下の図のように、頂点B,Dを結び、対角線を引きます。
辺BDは、三平方の定理(ピタゴラスの定理)より
\begin{align*}
BD^2 &= BC^2 + CD^2 \\
&= 1+ 1 \\
&= 2 \\
\Rightarrow \ BD &= \sqrt{2}
\end{align*}
となります。
この図から
\begin{cases}
\begin{align*}
\sin 45^\circ & = \frac{CD}{BD} = \frac{1}{ \sqrt{2} } \\
\cos 45^\circ & = \frac{BC}{BD} =\frac{1}{ \sqrt{2} } \\
\tan 45^\circ & = \frac{CD}{BC} = 1
\end{align*}
\end{cases}
であることがわかります。
三角比の拡張を行い、90度より大きい鈍角でも使えるように
直角三角形を用いた三角比の定義では、\( 0^\circ < \theta < 90^\circ \)の鋭角でしか三角比を定義することができません。
しかし、\( 0^\circ < \theta < 90^\circ \)の鋭角でしか三角比を定義できないのは、なにかと不便になってきます。
そこで、直角の場合や\( 90^\circ \)より大きい鈍角の場合でも三角比を使えるように拡張したのが、これから紹介する”単位円を使った定義”です。
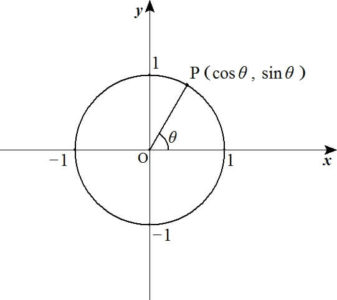
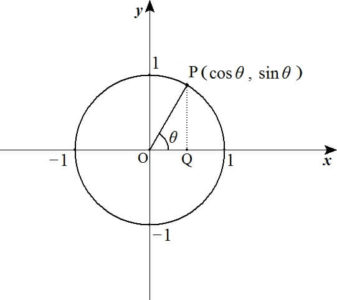
【三角比の定義(単位円を用いた定義)】
\( xy \)平面において、原点Oを中心に半径1の円(単位円)に点Pを取り、\( x \)軸と線分OPのなす角を\( \theta \)としたとき
- 点Pの\( x \)座標を\( \cos \theta \)
- 点Pの\( y \)座標を\( \sin \theta \)
- 線分OPの傾きを\( \tan \theta \)
と定義する。
このように定義することによって、\( 90^\circ \)以上の場合でも三角比を定義することができるようになります。
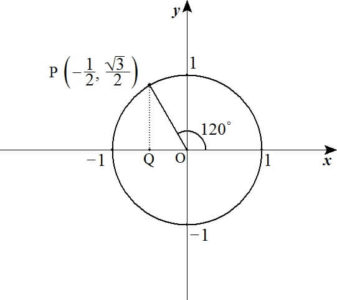
たとえば、\( \theta = 120^\circ \)の場合を考えてみましょう。
以下の図のように、点Pから\( x \)軸に垂線を引き、その交点をQとします。
そのときにできる\( 60^\circ \)の鋭角を持つ直角三角形OPQを考えると
\begin{align*}
PQ = \frac{ \sqrt{3} }{2} \\
OQ =\frac{1}{2}
\end{align*}
であることがわかります。
よって、点Pの\( x \)座標、\( y \)座標、傾きはそれぞれ
\begin{align*}
x \verb|座標:| & -\frac{1}{2} \\
y \verb|座標:| & \frac{ \sqrt{3} }{2} \\
\verb|傾き:| & -\sqrt{3}
\end{align*}
となります。
つまり、単位円を用いた三角比の定義より
\begin{align*}
\cos 120^\circ &= -\frac{1}{2} \\
\sin 120^\circ &=\frac{ \sqrt{3} }{2} \\
\tan 120^\circ &= -\sqrt{3}
\end{align*}
となります。
また、単位円を用いた定義でポイントになるのは、以下のことです。
\[ (r \cos \theta,r \sin \theta) \]
となる。

このように、定義を拡張することで、”正弦定理・余弦定理”を鈍角の場合でも使える、ということがあります。
それらの定理については、正弦定理・余弦定理の正しい使い方・解き方についてで詳しく説明していますので、合わせてご覧ください。
三角比の相互関係を表す式は、単位円を用いた定義を見ればすぐにわかる
三角比の相互関係を表す有名な式が3つあります。
【三角比の相互関係を表す3つの式】
\begin{align*}
& \tan \theta = \frac{\sin \theta}{\cos \theta} \\
& \sin^2 \theta + \cos^2 \theta = 1 \\
& \tan^2 \theta + 1 = \frac{1}{\cos^2 \theta}
\end{align*}
はじめは、これらの関係式のうち、1と2を理解していれば十分です。
3は主に数学Ⅲの積分という分野で使用しますので、そのときでも構いません。
これらの式の証明は、単位円を用いた三角比の定義からすぐに導かれます。
(1の証明)
単位円を用いた定義では、\( \tan \theta \)は線分OPの傾きを表しています。
線分OPの傾きは
\[ \frac{ y \verb|の変化量| }{ x \verb|の変化量| } \]
で求めることができます。
つまり
\begin{align*}
\tan \theta &= \frac{\sin \theta \ – 0 }{\cos \theta \ – 0} \\
&= \frac{\sin \theta}{\cos \theta}
\end{align*}
となります。
(2の証明)
単位円を使った三角比の定義では、単位円上の点Pの\( x \)座標は\( \cos \theta \)、\( y \)座標は\( \sin \theta \)でした。
いま、直角三角形OPQに注目すると
辺OQ = \( \cos \theta \)
辺PQ = \( \sin \theta \)
辺OP = \( 1 \)
であるから、三平方の定理を用いると
\[ \cos^2 \theta + \sin^2 \theta = 1 \]
が成り立ちます。
(3の証明)
2で証明した式
\[ \sin^2 \theta + \cos^2 \theta = 1 \]
の両辺を\( \cos^2 \theta \)で割ると
\begin{align*}
& \frac{ \sin^2 \theta }{ \cos^2 \theta } + 1 = \frac{ 1 }{ \cos^2 \theta } \\
\Leftrightarrow \ & (\frac{ \sin \theta }{ \cos \theta })^2 + 1 = \frac{ 1 }{ \cos^2 \theta }
\end{align*}
となります。
そして、この式に、1で証明した
\( \displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta} \)を用いると
\[ \tan^2 \theta + 1 = \frac{ 1 }{ \cos^2 \theta } \]
が導かれます。