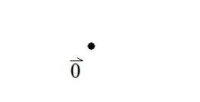ベクトルの分野では、”矢印”を扱うためのルールを学びます。
そのルールを理解すれば、後はちょっとしたコツで、図形や座標・方程式の問題を簡単に解くことができるようになります。
ここでは
- ベクトルとはなにか?
- ベクトルの扱い方・ルール
- ベクトルの表現方法
などのルールを紹介します。
ベクトルとは?
ベクトルとは、一言で言えば、”矢印”のことです。
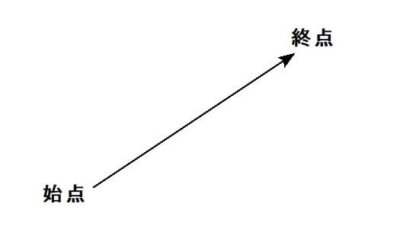
そして、ベクトルの世界では、矢印の根本の点を始点、先端の点を終点と言います。
ベクトルを\( a,b,c \)といった文字で表すときには、文字の上に右向きの矢印をつけて
\[ \vec{a},\vec{b},\vec{c} \]
と表します。
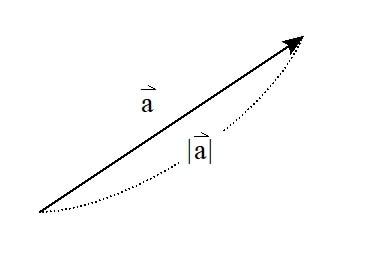
また、ベクトルの長さ(大きさ)は、絶対値の記号を用いて
\[ |\vec{a}| \]
と表します。
ベクトルの扱い方・ルール
ベクトルが等しいとは?
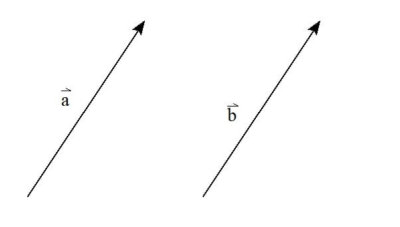
2つのベクトル\( \vec{a},\vec{b} \)の向きと長さが同じとき
\( \vec{a} \)と\(\vec{b} \)は等しい
といい、
\[ \vec{a} = \vec{b} \]
と表します。
向きも大きさも同じなので、
平行移動して重なるベクトルは等しい
と言えます。
逆ベクトルとは?
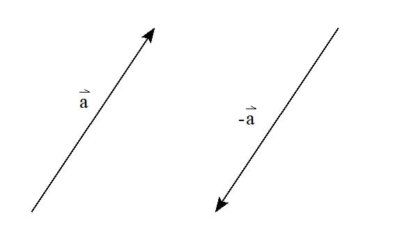
ベクトル\( \vec{a} \)と比べて、長さは同じで向きが反対のベクトルを
\( \vec{a} \)の逆ベクトル
といい、
\[ -\vec{a} \]
と表します。
ゼロベクトルとは?
長さが0のベクトルを
ゼロベクトル
といい、
\[ \vec{0} \]
と表します。
※図で表すと、矢印ではなく点になりますが、ベクトルの1種だと考えます。
ベクトルの実数倍
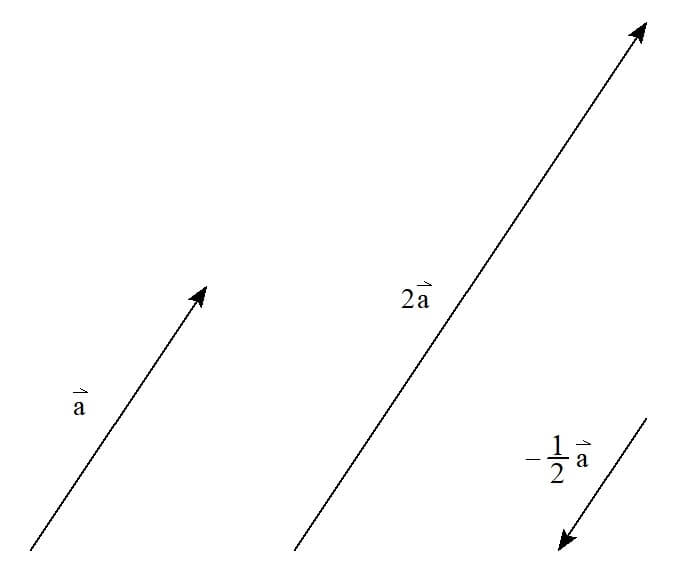
ベクトル\( \vec{a} \)に比べて、向きが同じで長さが2倍、3倍、4倍、…のベクトルは
\[ 2\vec{a}, 3\vec{a}, 4\vec{a}, \cdots\]
長さが1/2倍、1/3倍、…のベクトルであれば
\[ \frac{1}{2}\vec{a}, \frac{1}{3}\vec{a}, \cdots \]
と表します。
また、マイナスが付くと、逆ベクトルの場合と同様に向きが反対になります。
このように、ベクトルの実数倍は
矢印の拡大・縮小
になります。
ベクトルの足し算
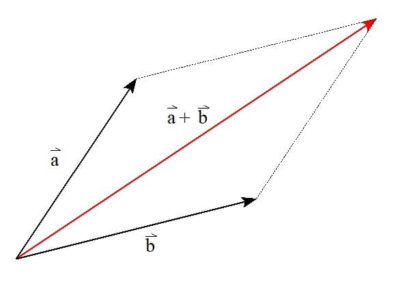
ベクトル\( \vec{a},\vec{b} \)の和\( \vec{a}+\vec{b} \)は、以下の図のように
始点を揃えて作った平行四辺形の対角線
になります。
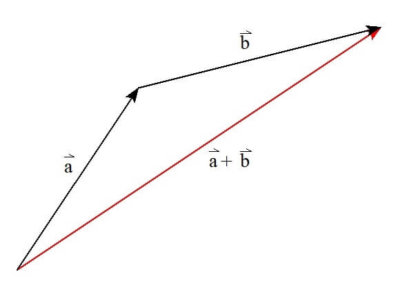
また、\( \vec{a}+\vec{b} \)は、以下の図のように
\( \vec{a} \)に\( \vec{b} \)を継ぎ足して作ったベクトル
と解釈することもできます。
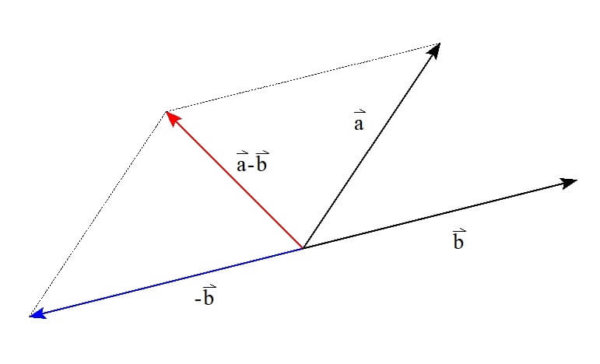
ベクトルの引き算
ベクトルの差\( \vec{a}-\vec{b} \)は、
\[ \vec{a}-\vec{b} = \vec{a}+ ( – \vec{b} ) \]
と書き換えることで、
\( \vec{a} \)に\( \vec{b} \)の逆ベクトルを足したベクトル
と考えることができます。
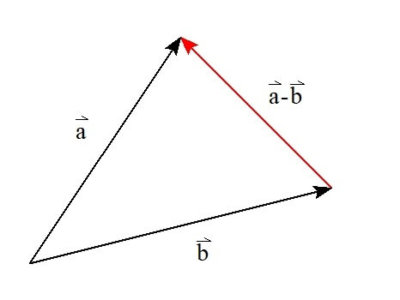
また、\( \vec{c} = \vec{a}-\vec{b} \)とすると
\begin{align}
& \vec{c} = \vec{a} – \vec{b} \\
\Leftrightarrow & \vec{c}+ \vec{b} = \vec{a} – \vec{b} + \vec{b} \\
\Leftrightarrow & \vec{c}+ \vec{b} = \vec{a} \\
\end{align}
と式変形することができます。
つまり、\( \vec{c} = \vec{a}-\vec{b} \)は、
\( \vec{b} \)を足せば\( \vec{a} \)になるベクトル
とも解釈することができます。
ベクトルを言葉で表す方法
ここまで、ベクトル(矢印)を扱ううえでのルールや計算方法を見てきました。
しかしながら、ただ矢印を書いただけでは、どんな矢印なのか他の人に正しく伝えることができません。
そこで、ベクトル(矢印)を言葉で表現する方法を考えてみましょう。
ここでは、
- 始点と終点の名前を用いる方法
- 座標を使って表現する方法(ベクトルの成分表示)
の2パターンを見ていきましょう。
始点と終点の名前を用いる方法
まずは、始点と終点の名前を用いる方法です。
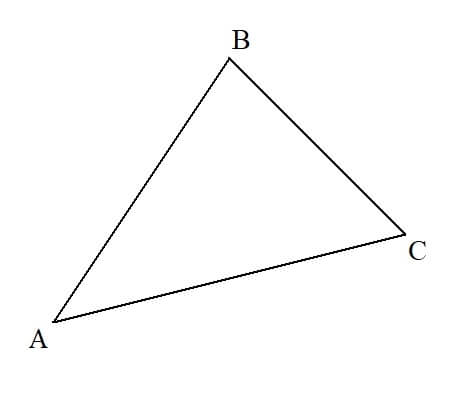
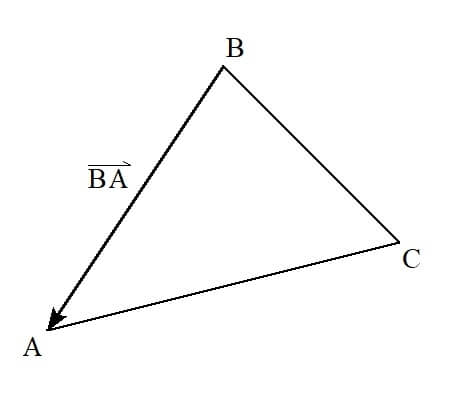
図形の問題で、三角形や四角形などの頂点に、「点A」というように名前が割り振られていることがよくあります。
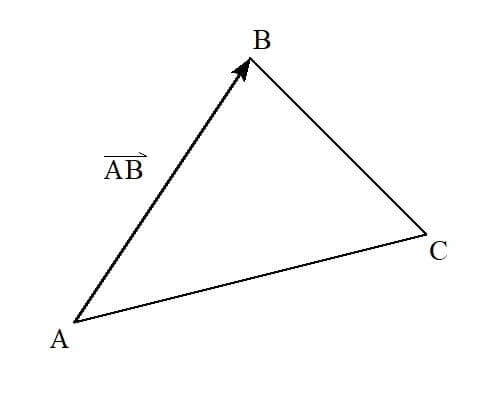
上記の図のようなとき、
- 向き:点Aから点Bの方向
- 長さ:線分ABと同じ長さ
というベクトル\( \vec{a} \)を、始点と終点の名前(ここでは、AとB)を使って
\[ \overrightarrow{ \mathrm{AB} } \]
と表すことができます。
また、文字の順番を入れ替えると、逆ベクトルになりますので注意してください。
座標を使って表現する方法
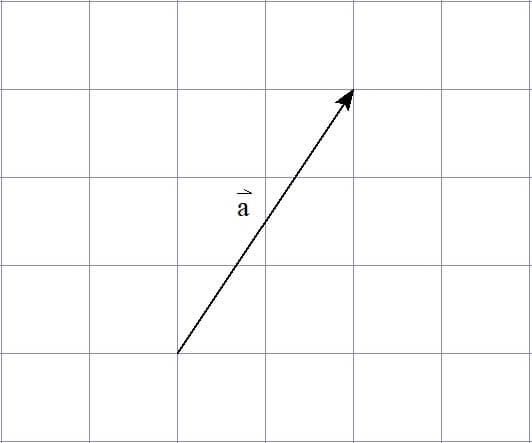
次は、座標を使って表現する方法です。
このように座標を用いると、ベクトル\( \vec{a} \)は
\( x \)軸方向に2、\( y \)軸方向に3のベクトル
ということができます。
このとき、ベクトル\( \vec{a} \)は
\[ \vec{a} = (2,3) \]
と表すことができます。
このような表し方を
ベクトルの成分表示
といいます。