みなさんは、”なぜ、合同条件を満たせば合同といえるのか、相似条件を満たせば相似といえるのか？”を考えたことがありますか？
ここで紹介する合同・相似への考え方は、これから学んでいく三角比や正弦定理・余弦定理を理解していくために必要な考え方になります。
中学校の復習の意味も込めて、ここで一度見直してみませんか？
ここでは
- 合同条件を満たすと、なぜ２つの三角形が合同といえるのか
- 相似条件を満たすと、なぜ２つの三角形が相似といえるのか
について、中学校ではあまり教えられてこなかったことを中心に説明いたします。
合同条件を満たすとなぜ合同なのか？を考えてみる
まずは、三角形の合同条件についての復習
まずは、”合同”についての復習です。
”合同”とは、簡単に言えば、２つの図形を比べたとき、形と大きさが同じであることをいいます。
言い換えると、一方の図形を動かしたり裏返したりすると、もう一方の図形に重ねることができるということです。
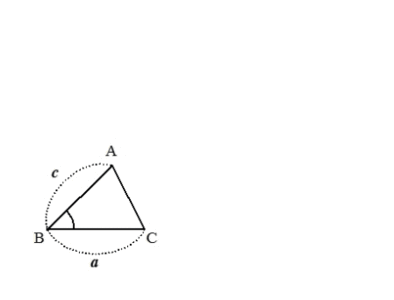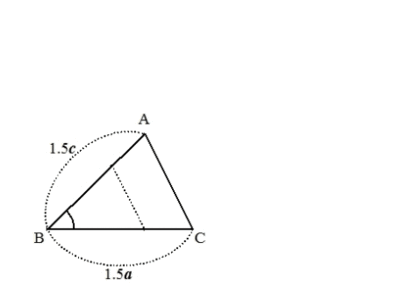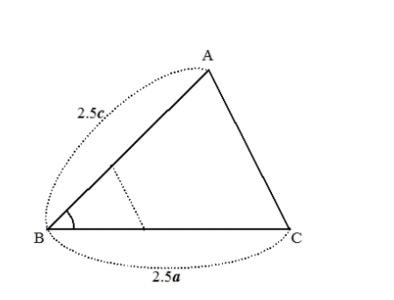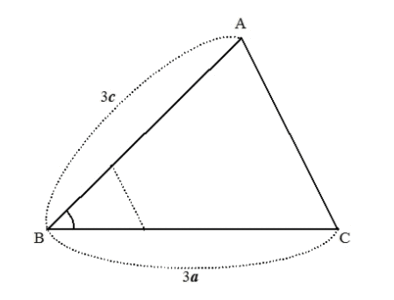
特に、三角形においては、次の１～３のいずれかの条件を満たせば、２つの三角形は合同であると言えます。
【三角形の合同条件】
- ３辺がすべて等しい
- ２辺とその間の角が等しい
- １辺とその両端の角が等しい
では、なぜこれらの条件を満たすと、２つの三角形が合同だと言えるのでしょうか？順番に見ていきましょう。
いくつかの条件が与えられると、三角形の大きさ・形がただ１通りに決まる
三角形の辺や角の大きさといった条件をいくつか与えると、その条件をみたす三角形がただひとつしか存在しない場合があります。
例えば、３辺の長さが決まると、その条件を満たす三角形はただひとつしかありません。
以下の図をみていただけると納得していただけるでしょうか？
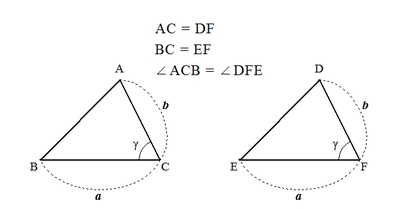
同様に、２辺の長さとその間の角が与えられると、その条件を満たす三角形はただひとつしかありません。
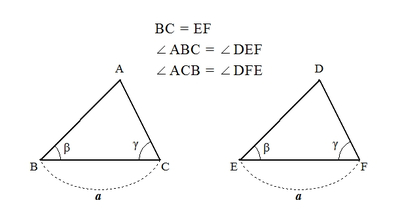
同様に、１辺の長さとその両端の角が与えられると、その条件を満たす三角形はただひとつしかありません。
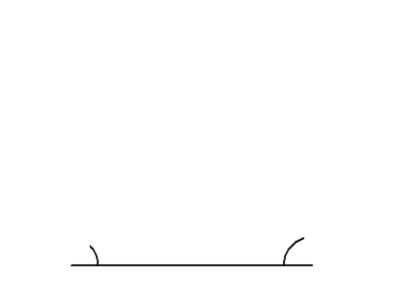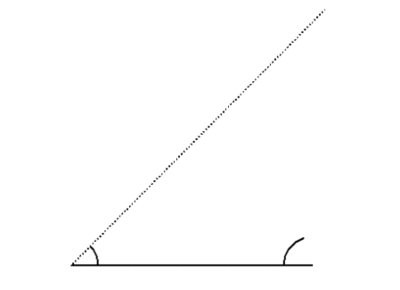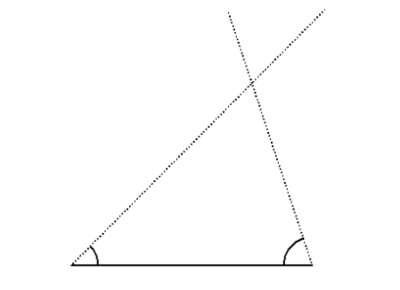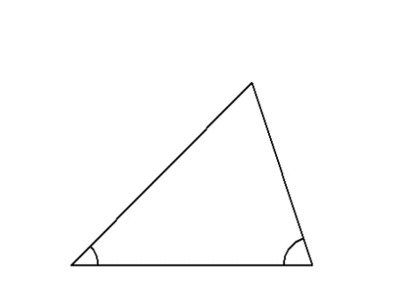
ここまで見てきたことを、以下にまとめておきます。
以下の１～３のいずれかのとき、三角形の大きさ・形がただ１通りに決まる。（各辺の長さ・角の大きさが１通りに決まる。）
- ３辺の長さが与えられたとき
- ２辺の長さとその間の角が与えられたとき
- １辺の長さとその両端の角が与えられたとき
（補足１） 三角形が１通りに決まらない例
上記のポイント１～３を見ると
三角形の辺や角度は６つあるから、そのうち３つの長さや角度が決まれば、三角形がただひとつに決まるのかな？
と思われるかもしれません。
しかし、辺や角度の条件が３つ与えられても、三角形がただ１通りに決まらない場合もあります。
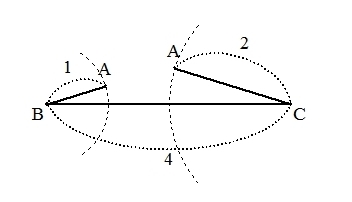
例えば、三角形ABCにおいて、２辺が与えられ、その間の角ではない角の大きさが与えられた場合です。（いま、辺 \( AB = c \)、辺\( AC = b \)、\( \angle ABC = \beta \)とします。）
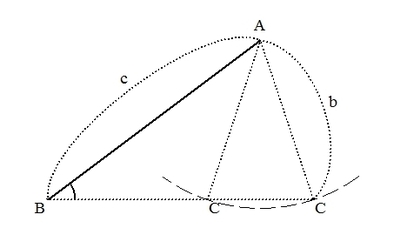
上記のような図を考えることによって、条件を満たす三角形が２つあることがわかります。
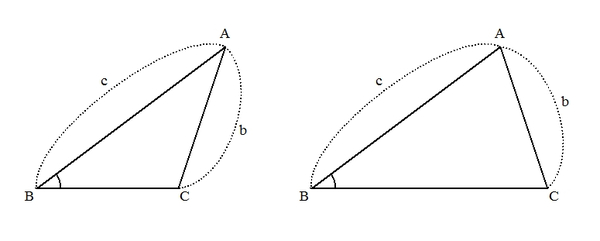
（補足２） 条件を満たす三角形が存在しない場合
ここまで、三角形がただひとつに決まる条件として以下の３つを紹介しました。
- ３辺の長さが与えられたとき
- ２辺の長さとその間の角度が与えられたとき
- １辺の長さとその両端の角度が与えられたとき
しかし、上記のような条件が与えられたとしても、その条件を満たす三角形が実際には存在しない場合もあります。
例えば三角形ABCにおいて、辺 \( AB = 1 \)、辺\( AC = 2 \)、辺\( BC = 4 \)の三角形は存在しません。
実際に、そのような辺を持った三角形を作図しようとするとわかります。（下記のような図になります。）
これまで、「三角形がただ１通りに決まる」といってきたのは、このような”三角形が存在しない”ということがない場合においてである、ということを念のため記しておきます。
１通りに決まるとき、同じ条件を与えられた２つの三角形は、合同になる
いよいよ、”三角形の合同条件を満たせば、なぜ合同であるのか？”の説明に入っていきます。
ここまで、三角形の大きさ・形がただ１通りに決まる条件には
- ３辺の長さが与えられたとき
- ２辺の長さとその間の角度が与えられたとき
- １辺の長さとその両端の角度が与えられたとき
の３つある、ということを見てきました。
ここで考えていただきたいのは、”三角形の大きさ・形がただ１通りに決まる条件を与えられた三角形ABCと三角形DEFにおいて、その与えられた条件がまったく同じだった場合、どうなるか？”ということです。
たとえば、三角形ABCについて、辺 \( AB = 6 \)、辺\( AC = 8 \)、\( \angle BAC = 60^\circ \)という条件が与えられたなら、三角形ABCはただ１通りに決まります。
言い換えれば、与えられた条件をみたす三角形は、ただひとつしか存在しないということです。
ここで、三角形DEFについても、辺 \( DE = 6 \)、辺\( DF = 8 \)、\( \angle EDF = 60^\circ \)と、三角形ABCと同じ条件が与えられたなら、どうでしょうか？
条件をみたす三角形は、ただひとつしか存在しないのですから、三角形ABCと三角形DEFは同じ三角形になるということはおわかりでしょうか？
つまり、”同じ条件が与えられた三角形ABCと三角形DEFにおいて、その条件をみたす三角形がただひとつしか存在しなければ、三角形ABCと三角形DEFは同じ三角形になる”ということです。
つまり、”三角形ABCと三角形DEFは合同である”ということになるのです。
相似条件を満たすとなぜ相似なのか？を考えてみる
まずは、三角形の相似条件についての復習
まずは、”相似”についての復習です。
”相似”とは、簡単に言えば、２つの図形の形が等しいことをいいます。
言い換えると、縮小・拡大した後、一方の図形を動かしたり裏返したりするともう一方の図形に重ねることができるということです。
特に、三角形においては、次の１～３のいずれかの条件を満たせば、２つの三角形は相似であると言えます。
【三角形の相似条件】
- ３辺の比がすべて等しい
- ２辺の比とその間の角が等しい
- ２角が等しい
では、なぜこれらの条件を満たすと、２つの三角形が合同だと言えるのでしょうか？順番に見ていきましょう。
いくつかの条件が与えられると、三角形の形がただ１通りに決まる
三角形の辺や角の大きさといった条件をいくつか与えると、その条件をみたす三角形の形がただひとつしか存在しない場合があります。
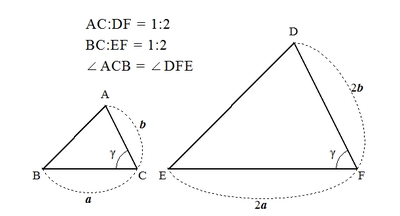
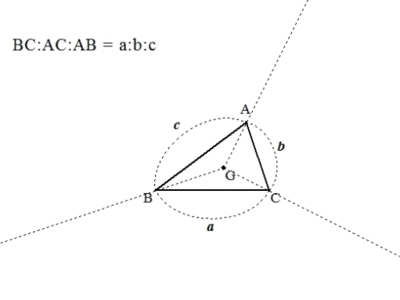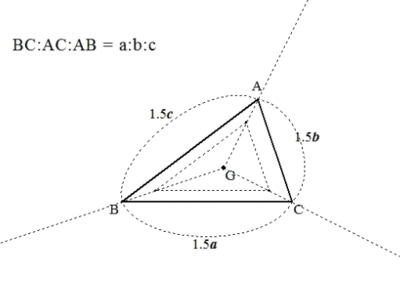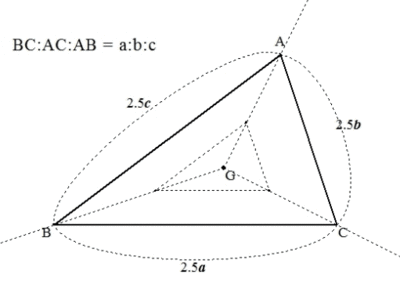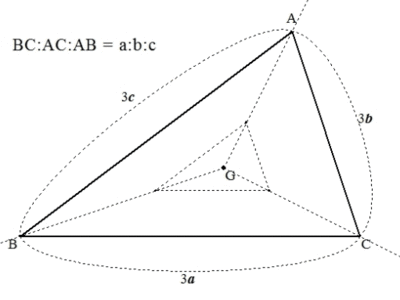
例えば、３辺の比が与えられると、その条件を満たす三角形の形はただ１通りに決まります。
以下の図をみていただけると納得していただけるでしょうか？
同様に、２辺の比とその間の角度が与えられると、その条件を満たす三角形の形はただ１通りに決まります。
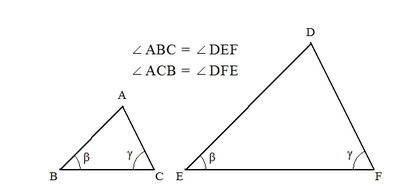
同様に、２つの角が与えられると、その条件を満たす三角形の形はただ１通りに決まります。
ここまで見てきたことを、以下にまとめておきます。
以下の１～３のいずれかのとき、三角形の形がただ１通りに決まる。（各辺の長さの比・角の大きさが１通りに決まる。）
- ３辺の比が与えられたとき
- ２辺の比とその間の角が与えられたとき
- ２つの角が与えられたとき
形が１通りに決まるとき、同じ条件を与えられた２つの三角形は、相似になる
最後に”三角形の相似条件を満たせば、なぜ相似であるのか？”の説明です。
ここまで、三角形の形がただ１通りに決まる条件には
- ３辺の比が与えられたとき
- ２辺の比とその間の角が与えられたとき
- ２つの角が与えられたとき
の３つある、ということを見てきました。
ここで考えていただきたいのは、合同のときと同じように、”三角形の形がただ１通りに決まる条件を与えられた三角形ABCと三角形DEFにおいて、その与えられた条件がまったく同じだった場合、どうなるか？”ということです。
合同のときと同じように考えれば、条件をみたす三角形は、ただひとつの形しか存在しないのですから、三角形ABCと三角形DEFは同じ形の三角形になるということです。
つまり、”三角形ABCと三角形DEFは相似である”ということになるのです。
こういった”合同・相似”の発想・考え方を用いれば、”三角比”や”正弦定理・余弦定理”の理解も深まります。
三角比については、三角比とは？定義の意味やポイントについてで詳しく説明していますので、合わせてご覧ください。