等比数列の一般項・和の公式とその応用（自然数×等比数列の和）について

こちらでは

\[ 3,6,12,24,48,\cdots \]

といったような、一定の数を掛けて作った”等比数列”について考えていきます。

等差数列の場合と同じように、まずは

• 一般項について
• 和の公式について

を説明します。

そして、応用問題として、等比数列の和の公式を導き出した考え方を使って

• ”自然数×等比数列”の形をした数列の和

についても考えていきます。

どの公式でも

と考えることが大事なのは、等比数列でも同じです。

等比数列の一般項の公式の導き方

等比数列とは

ある数に、次々と一定数を掛けていく

という規則に従って作られた数列のことをいいます。（次々に掛けていく数のことを”公比”といいます。）

言い換えれば

ひとつ前の数に一定数を掛けて作った数列

とも言えます。

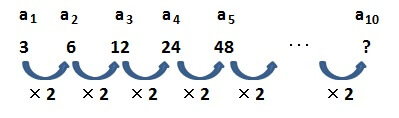
たとえば、冒頭であげた

\begin{align*}
3,6,12,24,48,\cdots
\end{align*}

は、初項\( 3 \)に、公比\( 2 \)を次々と掛けて作った数列です。

さて、この数列の10番目の数はいくつになるでしょうか？

この数列の関係性を表した以下の図を見ながら考えていきましょう。

この図から考えていただきたいのは、等差数列のところで見たのと同様に

\( a_1 \)との関係性

について。

\( a_2 \)、\( a_3 \)、\( a_4 \)、\( a_5 \)は、それぞれ\( a_1 \)に\( 2 \)を何回掛けた数でしょうか。

図からわかるように

\( a_2 \)は、\( a_1 \)に\( 2 \)を１回掛けた数
\( a_3 \)は、\( a_1 \)に\( 2 \)を２回掛けた数
\( a_4 \)は、\( a_1 \)に\( 2 \)を３回掛けた数
\( a_5 \)は、\( a_1 \)に\( 2 \)を４回掛けた数

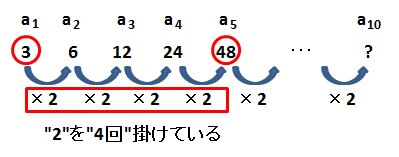
になっています。（下の図は、\( a_5 \)について強調したものです。）

それぞれの関係を、式で表せば次のようになります。

\begin{align*}
& a_2 = a_1 \cdot 2^1 \\
& a_3 = a_1 \cdot 2^2 \\
& a_4 = a_1 \cdot 2^3 \\
& a_5 = a_1 \cdot 2^4 \\
\end{align*}

同じように考えていくと

\( a_{10} \)は、\( a_{1} \)に\( 2 \)を９回掛けた数

になることがわかります。

つまり

\begin{align*}
a_{10} & = a_1 \cdot 2^9 \\
& = 3 \cdot 512 \\
& = 1536
\end{align*}

と求めることができます。

 

では、n番目の数はどのように表すことができるでしょうか。

10番目の数の場合と同じように

\( a_2 \)は、\( a_1 \)に\( 2 \)を１回掛けた数
\( a_3 \)は、\( a_1 \)に\( 2 \)を２回掛けた数
\( a_4 \)は、\( a_1 \)に\( 2 \)を３回掛けた数
\( a_5 \)は、\( a_1 \)に\( 2 \)を４回掛けた数
…
\( a_{10} \)は、\( a_1 \)に\( 2 \)を9回掛けた数
…

と考えていくと、

\( a_n \)は、\( a_1 \)に\( 2 \)をn-1回掛けた数

であることがわかります。

つまり、初項が\( 3 \)、公比\( 2 \)の数列\( \{ a_n \} \)の一般項\( a_n \)は

\begin{align*}
a_n & = 3 \cdot 2^{n – 1}
\end{align*}

と表すことができるのです。

 

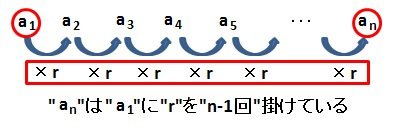
ここまでの復習も兼ねて、初項\( a_1 \)、公比\( r \)の等比数列の一般項\( a_n \)を考えてみましょう。

ここまで見てきたように考えれば、

\( a_n \)は、初項\( a_1 \)に公比\( r \)をn-1回掛けた数

といえます。

これを式にすると

\[ a_{n} = a_1 \cdot r^{n-1} \]

となるのです。

等比数列でも、等差数列と同じように

”\( a_n \)と\( a_1 \)との関係性”を意識する

ということが大事になります。

等比数列の和の公式の導き方（３通り）

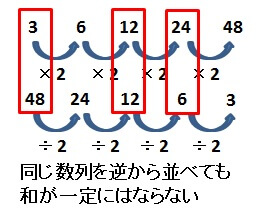
等比数列の一般項は、等差数列と同じように考えれば求めることができました。

と思いますが、等差数列とは違って、上下の和は一定になりません。

実際に、等比数列

\begin{align*}
3,6,12,24,48,\cdots
\end{align*}

で試してみましょう。

ここでは、簡単に初項から第５項までの和を考えてみます。

 

等差数列で使った方法がダメだったので、他の方法を考えるしかありません。

ここでは、以下の方法で等比数列の和の公式を導いていきます。

• いくつかの具体的な等比数列で、和を実際に計算し、予想を立てて証明する
• 和を\( r \)倍したものを引く
• 階差数列を利用して和を求める

 

まずは、ひとつ目の方法では、”いろいろな場合を考え、試行錯誤を繰り返し、予想を立てる”ということを繰り返して、等差数列の和の公式に迫っていきます。

こうした「実験 – 仮説 – 検証」というプロセスは、実際の試験でも役に立つ場面がたくさんあります。

ちょっとした練習だと思って、しばしお付き合いください。

※以下では、公比\( r \neq 0,1\)として考えていきます。

いろいろな等比数列を見て、等比数列の和の公式を予想する方法

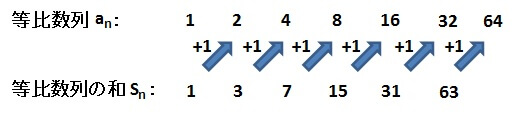
初項１、公比２の等比数列

まずは

初項1、公比2の等比数列

を考えてみましょう。

実際に書き表してみると

\[ 1,2,4,8,16,32,64, \cdots \]

ここで、具体的にいくつか和を計算してみましょう。

初項から第１項までの和は、当たり前ですが

\[ 1 \]

初項から第２項までの和は

\[ 1 + 2 = 3 \]

初項から第３項までの和は

\[ 1 + 2 + 4 = 7 \]

初項から第４項までの和は

\[ 1 + 2 + 4 + 8 = 15 \]

初項から第５項までの和は

\[ 1 + 2 + 4 + 8 + 16 = 31 \]

初項から第6項までの和は

\[ 1 + 2 + 4 + 8 + 16 + 32 = 63 \]

さて、なにかお気づきの点はないでしょうか。

元々の数列と、数列の和を並べてみると、見えてくるかもしれません。

元の等比数列：\( 1,2,4,8,16,32,64, \cdots \)
等比数列の和：\( 1,3,7,15,31,63, \cdots \)

そこで、以下のような予想を立てることができます。

この【予想１】は、正しいのでしょうか？

他の等比数列の和も考えてみましょう。

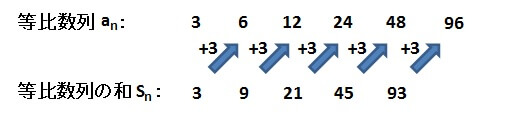
初項３、公比２の等比数列

次は、初項の値を変えて

初項3、公比2の等比数列

を考えてみましょう。

書き出してみると

\[ 3,6,12,24,48,96, \cdots \]

そして、初項から第１項までの和は

\[ 3 \]

初項から第２項までの和は

\[ 3 + 6 = 9 \]

初項から第３項までの和は

\[ 3 + 6 + 12 = 21 \]

初項から第４項までの和は

\[ 3 + 6 + 12 + 24 = 45 \]

初項から第５項までの和は

\[ 3 + 6 + 12 + 24 + 48 = 93 \]

さて、元々の数列と、数列の和を並べてみましょう。

元の等比数列：\( 3,6,12,24,48,96, \cdots \)
等比数列の和：\( 3,9,21,45,93, \cdots \)

最初に試したのは、

初項１で、和より１だけ大きい数字が元の数列に現れている

ここで試したのは

初項３で、和より３だけ大きい数字が元の数列に現れている

つまり

和は初項の分だけ小さくなるのではないか？

という予測が立てられそうです。

こうやって考えると、次のような新しい予想を立てることができます。

【予想１】は外れてしまいましたが、【予想２】はどうでしょうか？

さらに、他の等比数列の和も考えてみましょう。

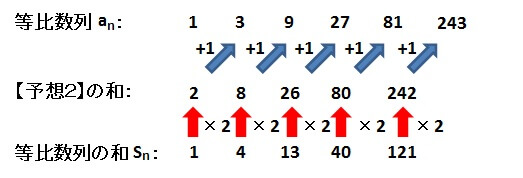
初項１、公比３の等比数列

今度は公比を変えて

初項1、公比３の等比数列

を考えてみましょう。

この数列は

\[ 1,3,9,27,81,243 \cdots \]

と書き表すことができます。

そして、初項から第１項までの和は

\[ 1 \]

初項から第２項までの和は

\[ 1 + 3 = 4 \]

初項から第３項までの和は

\[ 1 + 3 + 9 = 13 \]

初項から第４項までの和は

\[ 1 + 3 + 9 + 27 = 40 \]

初項から第５項までの和は

\[ 1 + 3 + 9 + 27 + 81 = 121 \]

となります。

なにやら、いままでと様子が少し違います。

【予想２】が正しければ、等比数列の和は

\[ 2,8,26,80,242, \cdots \]

となっているはずでした。

しかし、実際は

\[ 1,4,13,40,121, \cdots \]

となっています。

一度、これらの数列を並べてみましょう。

元の等比数列　：\( 1,3,9,27,81,243 \cdots \)
予想していた和：\( 2,8,26,80,242, \cdots \)
実際の和　　　：\( 1,4,13,40,121, \cdots \)

こうやって並べてみると気づくことはありませんか？

これは、どういうことでしょうか。

最初に試してわかったことは、

公比２の場合、和の１倍より初項１の分だけ大きい数字が元の数列になっている

ということ。

ここで試してわかったことは、

公比３の場合、和の２倍より初項１の分だけ大きい数字が元の数列になっている

ということです。

つまり

初項から第n項までの和は、第n+1項の数から初項の分だけ引き、さらに公比より１小さい数で割っているのではないか？

と推測できます。

【予想２】も外れてしまいましたが、新たな予想を立てることができました。

さて、この【予想３】は正しいのでしょうか？

初項３、公比４の等比数列

次は

初項３、公比４の等比数列

を考えてみましょう。

この数列は

\[ 3,12,48,192,768,3072, \cdots \]

と書き表すことができます。

そして、初項から第１項までの和は

\[ 3 \]

初項から第２項までの和は

\[ 3 + 12 = 15 \]

初項から第３項までの和は

\[ 3 + 12 + 48 = 63 \]

初項から第４項までの和は

\[ 3 + 12 + 48 + 192 = 255 \]

初項から第５項までの和は

\[ 3 + 12 + 48 + 192 + 768 = 1023 \]

 

元の等比数列：\( 3,12,48,192,768,3072, \cdots \)
等比数列の和：\( 3,15,63,255,1023, \cdots \)

並べてみると、【予想３】の式

\[ S_n = \frac{1}{r – 1}(a_{n+1} – a_{1}) \]

が成り立っているのがわかります。

実際に

和の数列の第４項目は

\[ S_4 = 255 \]

元の数列の第５項目と初項の差は

\[ a_5 – a_1 = 765 \]

ですので

\begin{align*} \\
& \frac{1}{4-1} (a_5 – a_1) \\
& = \frac{1}{3} \cdot 765 \\
& = 255
\end{align*}

となり、【予想３】が成り立っています。

そこで

初項\( a \)、公比\( r \)の等比数列

を考えて、どんな場合でも【予想３】が成り立つのか確かめてみましょう。

初項\( a \)、公比\( r \)の等比数列

ここまでいくつかの等比数列を考えてきて、私たちが導き出した【予想３】は、以下のものでした。

この予想した式がどんな等比数列でも成り立つのでしょうか？

初項\( a \)、公比\( r \)の等比数列

\[ a_n = a \cdot r^{n-1} \]

を考えていきましょう。

まずは、左辺の\( S_n \)から。

左辺の\( S_n \)は、項から第n項までの和なので

\begin{align*}
S_n = & a + a \cdot r + a \cdot r^2 + \cdots + a \cdot r^{n-1} \\
= & a(1 + r + r^2 + \cdots + r^{n-1}) \\
\end{align*}

と表せます。

次に右辺の式を考えていきましょう。

右辺の式は

\begin{align*}
& \frac{1}{r – 1}(a \cdot r^n – a) \\
= & \frac{1}{r – 1}a(r^n – 1) \\
\end{align*}

と表すことができます。

また、\( r^n – 1 \)は、以下のように因数分解できます。

\begin{align*}
& r^n – 1 \\
= & ( r -1 )(r^{n-1} + r^{n-2} + \cdots + r^2 + r + 1)
\end{align*}

つまり、右辺の式は、さらに

\begin{align*}
& \frac{1}{r – 1}a(r^n – 1) \\
= & \frac{1}{r – 1}a( r -1 )(r^{n-1} + \cdots + r^2 + r + 1) \\
= & a(r^{n-1} + r^{n-2} + \cdots + r^2 + r + 1)
\end{align*}

と式変形ができ、左辺の式と等しくなりました。

つまり、等比数列の和の公式は、予想していた

\[ S_n = \frac{1}{r – 1}(a_{n+1} – a_{1}) \]

という式で正しかったのです。

また、等比数列の一般項は

\[ a_n = a_1 \cdot r^{n-1} \]

と表せるので、和の公式は

\begin{align*}
S_n & = \frac{1}{r – 1}(a_1 \cdot r^n – a_{1}) \\
& = \frac{a_1 ( r^n – 1)}{r – 1}
\end{align*}

とも表すことができます。

※予想した式が正しいことを証明するには

「予想した式の（左辺）-（右辺）を計算し、0になることを確かめる」

という手順で行っても構いません。

（途中に出てきた因数分解を思いつかなくても、機械的に計算していくと証明できるので、一度試してみてください）

和を\( r \)倍したものを引いて等比数列の和を求める方法

さて、ふたつ目の方法の

”和を\( r \)倍して引く方法”

に入っていきましょう。

この”和を\( r \)倍して引く”は、教科書や参考書に載っている方法です。

この方法のポイントは

公比\( r \)を掛けると”第２項から第n+1項が現れる”

ということ。

具体的な手順を見ていきましょう。

まず、初項\( a_1 \)、公比\( r \)の等比数列を\( \{ a_n \} \)、その数列の初項から第n項までの和を\( S_n \)とします。

すると、\( S_n \)は

\begin{align*}
S_n = a_1 + a_1 \cdot r + a_1 \cdot r^2 + \cdots + a_1 \cdot r^{n-1}
\end{align*}

と表すことができます。

ここで\( S_n \)に公比の\( r \)を掛けた式を考えてみましょう。

\begin{align*}
rS_n = & \ a_1 \cdot r + a_1 \cdot r^2 \\
& + \cdots + a_1 \cdot r^{n-1} + a_1 \cdot r^{n} \\
\end{align*}

この\( rS_n \)は

元の数列\( \{ a_n \} \)の第２項から第n+1項までの和

になっています。

そこで、\( rS_n – S_n \)を計算すると、どういうことが起こるでしょうか。

元の数列の第２項\( a \cdot r \)から第n項\( a \cdot r^{n-1} \)までが消えてしまうのです。

実際に計算すると

\begin{align*}
& rS_n – S_n \\
= & a_1 \cdot r + a_1 \cdot r^2 + \cdots + a_1 \cdot r^{n-1} + a_1 \cdot r^{n} \\
& – (a_1 + a_1 \cdot r + a_1 \cdot r^2 + \cdots + a_1 \cdot r^{n-1}) \\
= & a_1 \cdot r^{n} – a_1
\end{align*}

となり、初項と第n+1項だけが残りました。

よって、両辺を整理すると

\begin{align*}
& rS_n – S_n = a_1 \cdot r^{n} – a_1 \\
\Leftrightarrow \ & ( r – 1 )S_n = a_1( r^{n} – 1 ) \\
\Leftrightarrow \ & S_n = \frac{a_1( r^{n} – 1 )}{ r – 1 }
\end{align*}

となり、等比数列の和の公式を求めることができました。

階差数列を利用して等比数列の和を求める方法

最後の方法は、

等比数列の階差数列を利用する方法

です。

※前提知識として、「階差数列の定義や利用・活用について」にて紹介している

• 等比数列の階差数列もまた等比数列になる
• 和を求めたい数列が階差数列となるような数列を見つけられれば、和は計算できる

といったことを使用しています。

 

さて、初項\( a \)、公比\( r \)の等比数列

\[ b_n = ar^{n-1} \]

の和を、階差数列の考え方を利用して求めていきましょう。

和を求めるのに必要なものは

階差を計算すると、\( ar^{n-1} \)となるような数列

です。

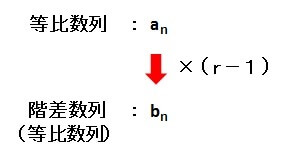
そのような数列を求めるときに役立つのが

公比 r の等比数列の階差数列は、(r – 1)倍の等比数列になる

ということです。

このことを逆に見ると

公比 r の等比数列を階差数列にもつ数列は、\( \displaystyle \frac{1}{r-1} \)倍の等比数列である

ということが言えるのです。

つまり、等比数列\( \{ b_n \} \)を階差数列にもつ数列は、\( \frac{1}{r-1} \)倍した

\[ a_n = \frac{1}{r-1} ar^{n-1} \]

です。

そして、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は

\begin{align*}
\sum_{k=1}^{n} b_n & = a_{n+1} – a_1
\end{align*}

と表せます。

つまり、初項 a 、公比 r の等比数列の和は

\begin{align*}
\sum_{k=1}^{n} ar^{n-1} & = a_{n+1} – a_1
\end{align*}

となります。

この右辺を計算していくと

\begin{align*}
& a_{n+1} – a_1 \\
= & \frac{1}{r-1} ar^n – \frac{1}{r-1} ar^0 \\
= & \frac{1}{r-1} a(r^n – 1)
\end{align*}

となり、等比数列の和の公式を求めることができるのです。

”自然数×等比数列”の形をした数列の和を求めてみる

最後に、応用問題として、”自然数×等比数列”の形をした

\[ a_n = n \cdot ar^{n-1} \]

という数列の初項から第n項までの和\( S_n \)を求めてみましょう。

ここでは

• 等比数列の和が複数あると考えて計算する方法
• 和を\( r \)倍して引く方法

の２通りの方法で求めていきます。

等比数列の和が複数あると考えて計算する方法

まず、ひとつ目の

”等比数列の和が複数あると考えて計算する方法”

を紹介いたします。

まずは、和がどんな形になっているか把握するために、求めたい和を具体的に書いてみましょう。

\begin{align*}
S_n = & 1 \cdot a + 2 \cdot ar + 3 \cdot ar^2 \\
& + \cdots + ( n – 1 ) \cdot ar^{n-2} + n \cdot ar^{n-1}
\end{align*}

この式を見て

なんて思いましたか？

実は、この式には、等比数列の和がいくつも隠れているのです。

私たちが求めることができる等比数列の和は

\[ a + ar + ar^2 + \cdots + ar^{n-1} + ar^{n} \]

という形。

そこで、いま邪魔になるのは、\( 2 ar \)の\( 2 \)のような、前についている自然数。

しかし、見方を変えると

\( 2 ar \)は、\( ar \)が２つある

と考えることができます。

つまり

\[ 2 ar = ar + ar \]

と書くことができます。

他の\( 3 ar^2 \)や\( n ar^{n-1} \)でも同様です。

そうすると、いま求めたい和\( S_n \)は

\begin{align*}
a + ar + ar^2 + & \cdots + ar^{n-2} + ar^{n-1} \\
+ ar + ar^2 + & \cdots + ar^{n-2} + ar^{n-1} \\
+ ar^2 + & \cdots + ar^{n-2} + ar^{n-1} \\
& \vdots \\
& \phantom{ \cdots } + ar^{n-2} + ar^{n-1} \\
& \phantom{ \cdots + ar^{n-2} } + ar^{n-1}
\end{align*}

と書き直すことができます。

この式を縦に見ると

初項の\( a \)が１個
第２項の\( ar \)が２個
第３項の\( ar^2 \)が３個
…
第n項の\( ar^{n-1} \)がｎ個

と並んでいますので、元の式と同じことが確かめられます。

そして、この式は横に見ると

１行目は

初項\( a \)、公比\( r \)の等比数列の初項から第ｎ項までの和

２行目は

初項\( ar \)、公比\( r \)の等比数列の初項から第ｎ-1項までの和

３行目は

初項\( ar^2 \)、公比\( r \)の等比数列の初項から第ｎ-2項までの和

…

ｎ-1行目は

初項\( ar^{n-2} \)、公比\( r \)の等比数列の初項から第２項までの和

ｎ行目は

初項\( ar^{n-1} \)、公比\( r \)の等比数列の初項から初項までの和

となっています。

等比数列の初項から第ｎ項までの和が

\[ \frac{1}{r – 1}(a_{n+1} – a_{1}) \]

と表せるので

１行目は

\[ \frac{a}{r – 1}(r^{n} – 1) \]

２行目は

\[ \frac{a}{r – 1}(r^{n} – r) \]

３行目は

\[ \frac{a}{r – 1}(r^{n} – r^2) \]

…

ｎ-1行目は

\[ \frac{a}{r – 1}(r^{n} – r^{n-2}) \]

ｎ行目は

\[ \frac{a}{r – 1}(r^{n} – r^{n-1}) \]

と表せます。

いま求めたい和\( S_n \)は、これらの行の和ですから

\begin{align*}
& \frac{a}{r – 1}(r^{n} – 1) + \frac{a}{r – 1}(r^{n} – r) + \frac{a}{r – 1}(r^{n} – r^2) \\
& \ + \cdots + \frac{a}{r – 1}(r^{n} – r^{n-2}) + \frac{a}{r – 1}(r^{n} – r^{n-1}) \\
= & \frac{a}{r – 1}\{ nr^{n} – (1 + r + r^2 + \cdots + r^{n-1}) \}
\end{align*}

となります。

さらに、\( 1 + r + r^2 + \cdots + r^{n-1} \)も初項１、公比\( r \)の等比数列なので

\[ \frac{1}{r – 1}(r^{n} – 1) \]

と表せますので、求めたい和\( S_n \)は

\begin{align*}
& \frac{a}{r – 1}\{ nr^{n} – \frac{1}{r – 1}(r^{n} – 1) \} \\
= & \frac{a}{(r – 1)^2}\{ nr^{n}(r-1) – (r^{n} – 1) \} \\
= & \frac{a}{(r – 1)^2}( nr^{n+1} – nr^{n} – r^{n} + 1 ) \\
= & \frac{a}{(r – 1)^2}( nr^{n+1} – (n+1)r^{n} + 1 ) \\
\end{align*}

と表すことができるのです。

和を\( r \)倍して引く方法

自然数×等比数列の形をした数列でも、等比数列の和を求めた

”和を\( r \)倍して引く”

という方法は、有効な手段になります。

実際にやってみましょう。

求めたい和\( S_n \)は

\begin{align*}
S_n = & 1 \cdot a + 2 \cdot ar + 3 \cdot ar^2 \\
& + \cdots + ( n – 1 ) \cdot ar^{n-2} + n \cdot ar^{n-1}
\end{align*}

ですので、公比？にあたる\( r \)を掛けてみると

\begin{align*}
rS_n = & 1 \cdot ar + 2 \cdot ar^2 + 3 \cdot ar^3 \\
& + \cdots + ( n – 1 ) \cdot ar^{n-1} + n \cdot ar^{n}
\end{align*}

すると

\( ar \),\( ar^2 \),\( ar^3 \),\( \cdots \),\( ar^{n-2} \),\( ar^{n-1} \)のそれぞれの係数が、求めたい和\( S_n \)のそれぞれの係数と比べて、ひとつ小さくなっている

ことがわかります。

つまり

\( rS_n \)と\( S_n \)の差を取ると、\( ar \),\( ar^2 \),\( ar^3 \),\( \cdots \),\( ar^{n-2} \),\( ar^{n-1} \)の係数がすべて１

になるのです。

実際に、\( rS_n -S_n \)は

\begin{align*}
& \phantom{-(} 1 \cdot ar + 2 \cdot ar^2 + 3 \cdot ar^3 \\
& \phantom{-(1} + \cdots + ( n – 1 ) \cdot ar^{n-1} + n \cdot ar^{n} \\
& -(1 \cdot a + 2 \cdot ar + 3 \cdot ar^2 \\
& \phantom{-(1}+ \cdots + ( n – 1 ) \cdot ar^{n-2} + n \cdot ar^{n-1} ) \\
& = \  n \cdot ar^{n} \\
& \phantom{-(1} – a(1 + r + r^2 + \cdots + r^{n-2} + r^{n-1}) \\
\end{align*}

と表せます。

そして、\( 1 + r + r^2 + \cdots + r^{n-2} + r^{n-1} \)は、初項\( 1 \)、公比\( r \)の等比数列の初項から第ｎ項までの和なので

\[ \frac{1}{r – 1}(r^n – 1) \]

となります。

つまり、\( rS_n -S_n \)は

\begin{align*}
& n \cdot ar^{n} – \frac{a}{r – 1}(r^n – 1) \\
= & \frac{a}{r-1}\{ n \cdot r^{n}(r-1) – (r^n – 1) \} \\
= & \frac{a}{r-1}( n \cdot r^{n+1} – n \cdot r^{n} – r^n + 1 ) \\
= & \frac{a}{r-1}\{ n \cdot r^{n+1} – (n+1) \cdot r^{n} + 1 \}
\end{align*}

となります。

つまり

\begin{align*}
& rS_n -S_n \\
& = \frac{a}{r-1}\{ n \cdot r^{n+1} – (n+1) \cdot r^{n} + 1 \} \\
\Leftrightarrow & \ (r-1)S_n \\
& = \frac{a}{r-1}\{ n \cdot r^{n+1} – (n+1) \cdot r^{n} + 1 \} \\
\Leftrightarrow & \ S_n \\
& = \frac{a}{(r-1)^2}\{ n \cdot r^{n+1} – (n+1) \cdot r^{n} + 1 \} \\
\end{align*}

となります。