ここで紹介する階差数列とは、簡単に言ってしまうと、
数列の隣り合う項の差をとって作られる数列
です。
そんな単純な規則で作られる数列なのに、階差数列を考えることでおもしろい事実がいろいろわかってきます。
ここでは、まず”階差数列の定義”を説明します。
そして、階差数列を考えることで判明する興味深い事柄をいくつか紹介します。
具体的には
- 等比数列の階差数列もまた等比数列になる
- nのm次式で表される数列の階差数列は、nの(m-1)次式で表される数列になる
- 階差数列の和が求められるなら、元々の数列の一般項が求められる
- 和を求めたい数列が階差数列となるような数列を見つけられれば、和は計算できる
といった事柄がわかります。
これらの事柄は、自然数のm乗の和
\[ \sum_{k=1}^{n} k^m \ (m = 1,2,3,\cdots) \]
を考えるうえで役に立ちますので、しっかりと見ていきましょう。
階差数列の定義について
まずは、具体的な数列を通じて、階差数列を見ていきましょう。
よく例としてあげられる
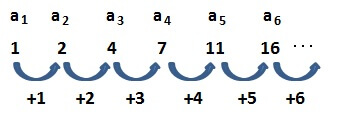
\[ a_n:1,2,4,7,11,16, \cdots \]
を見てみましょう。
この数列は、どのように変化しているでしょうか。
以下の図のように見ると、\( 1,2,3,4,5,6 \)と増加していることがわかります。
そして、”いくつ増加したか”を並べた数列
\[ b_n :1,2,3,4,5,6,\cdots \]
のことを、元の数列\( \{ a_n \} \)の”階差数列”といいます。
ここでは、階差数列は
\[ b_n = n \]
となっています。
そして、”いくつ増加したか”は、\( a_{n+1} – a_{n} \)を計算すると出てきます。
このように、数列\( \{ a_n \} \)に対して、隣り合う項の増加量
\[ b_n = a_{n+1} – a_n \]
を並べた数列\( \{ b_n \} \)のことを、数列\( \{ a_n \} \)の階差数列といいます。
数列\( \{ a_n \} \)に対して
\[ b_n = a_{n+1} -a_{n} \]
と、各項の差をとって作られる数列\( \{ b_n \} \)のことを、数列\( \{ a_n \} \)の階差数列という。

ただ各項の差をとって並べただけやんか!
と思われましたか?
でも、この”変化した量を考える”という考え方をすると、わかることがたくさんあるのです。
ひとつひとつ見ていきましょう。
階差数列を考えることでわかる4つのこと
教科書では、あまり大きく取り上げられない階差数列ですが、実は階差数列を利用することでいろいろなことがわかるのです。
ここでは、
- 等比数列の階差数列は、(r – 1)倍の等比数列になる
- m次式の数列の階差数列は、(m-1)次式の数列になる
- 階差数列の和が求められるなら、元の数列の一般項が求められる
- 和を求めたい数列が階差数列となるような数列を見つけられれば、和は計算できる
の4つをご紹介いたします。
等比数列の階差数列は、(r – 1)倍の等比数列になる
まずは、
等比数列の階差数列は、(r – 1)倍の等比数列になる
ということを見ていきましょう。
これは、実際に等比数列の階差数列を計算してみるとわかります。
また、このことを知っていると、教科書で紹介されている方法とは違ったやり方で、等比数列の和を求められるようになります。
初項が\( a \)、公比が\( r \)の等比数列を計算してみる
実際に、等比数列の階差数列を計算して確かめてみましょう。
ここでは、
初項が\( a \)、公比が\( r \)の等比数列を\( \{ a_n \} \)、その数列の階差数列を\( \{ b_n \} \)とします。
※\( r = 1 \)の場合、定数数列になってしまうので、ここでは\( r \neq 1 \)とします。
等比数列\( \{ a_n \} \)の一般項は
\[ a_n = ar^{n-1} \]
と表せるので、その階差数列\( \{ b_n \} \)は
\begin{align*}
b_n = & a_{n+1} – a_n \\
= & ar^n – ar^{n-1} \\
= & ar^{n-1}(r-1) \\
= & a(r-1)r^{n-1} \\
\end{align*}
となります。
ここから
階差数列\( \{ b_n \} \)は、初項\( a(r-1) \)、公比\( r \)の等比数列である
ということがわかります。
つまり、階差数列\( \{ b_n \} \)は、元の数列\( \{ a_n \} \)と比べると
- 初項が\( (r-1) \)倍になっている
- 公比が\( r \)で同じ
ということがわかります。
また、\( a_n = ar^{n-1} \)であるので、\( b_n \)は
\begin{align*}
b_n = & \underline{ ar^{n-1} } (r-1) \\
= & a_n (r-1)
\end{align*}
と表すことができます。
つまり
階差数列\( \{ b_n \} \)は、元の等比数列\( \{ a_n \} \)の\( (r-1) \)倍
になっているのです。
このことと、後に紹介する「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」を用いれば、教科書とは違った方法で等比数列の和を求めることができるようになります。
m次式の数列の階差数列は、(m-1)次式の数列になる
次は、
m次式で表される数列の階差数列は、(m-1)次式で表される数列になる
ということです。
ここでは、
- 2次式の階差数列
- 3次式の階差数列
- m次式の階差数列
を実際に計算して確かめていきます。
また、このことを知っていると
どのような数列を利用すれば、2乗の和、3乗の和、…を求めることができるか?
ということを理解することができます。
2次式の階差数列は、1次式になる
まずは、nの2次式で表される数列
\[ a_n = an^2 + bn + c \]
の階差数列を実際に計算してみましょう。
この数列\( \{ a_n \} \)の階差数列は
\begin{align*}
a_{n+1} – a_n = & a(n+1)^2 + b(n+1) + c \\
& \ – (an^2 + bn + c) \\
= & an^2 + 2an + a + bn + b + c \\
& \ – an^2 – bn – c \\
= & 2an + a + b
\end{align*}
と\( n^2 \)の項が消えて、nの1次式となります。
つまり
nの2次式で表される数列の階差数列は、nの1次式で表される
ということが示されました。
3次式の階差数列は、2次式になる
次に、nの3次式で表される数列
\[ a_n = an^3 + bn^2 + cn + d \]
の階差数列を実際に計算してみましょう。
この数列\( \{ a_n \} \)の階差数列は
\begin{align*}
& a_{n+1} – a_n \\
= & a(n+1)^3 + b(n+1)^2 + c(n+1) + d \\
& \ – (an^3 + bn^2 + cn + d ) \\
= & an^3 + 3an^2 + 3an + a \\
& + bn^2 + 2bn + a \\
& + cn + c + d \\
& \ – an^3 – bn^2 – cn – d \\
= & 3an^2 + 3an + a \\
& + 2bn + b + c \\
= & 3an^2 + ( 3a + 2b )n + b + c
\end{align*}
と\( n^3 \)の項が消えて、nの2次式となります。
つまり
nの3次式で表される数列の階差数列は、nの2次式で表される
ということが示されました。
m次式の階差数列は、(m – 1)次式になる
ここまで
- 2次式の階差数列は、1次式になる
- 3次式の階差数列は、2次式になる
といったことを見てきました。
これは、4次式になっても5次式になっても変わりません。
そこで最後に、より一般的に
m次式の階差数列は、(m – 1)次式になる
ということを見ていきます。
ここでは、m次式
\[ a_n = \alpha_m n^m + \alpha_{m-1} n^{m-1} + \cdots + \alpha_1 n + \alpha_0 \]
で表される数列を使って、階差数列が(m – 1)次式になることを見ます。

ちょっと待って!\( a_n – a_{n-1} \)を計算するの?めちゃくちゃ大変じゃない?
と思われた方もおられると思います。
しかし、階差数列が(m – 1)次式になることを見るだけなら、すべて計算する必要はありません。
階差数列を計算したとき、\( n^m \)の項が消えることが確認できればいいのです。
つまり、すべての項について計算する必要はなく、\( n^m \)の項だけを計算すればいいということです。
階差数列は
\begin{align*}
& a_n – a_{n-1} \\
= & \underline{\alpha_m n^m} + \alpha_{m-1} n^{m-1} + \cdots + \alpha_1 n + \alpha_0 \\
& \underline{ – \alpha_m (n-1)^m } – \alpha_{m-1} (n-1)^{m-1} – \cdots \\
& – \cdots – \alpha_1 (n-1) – \alpha_0 \\
\end{align*}
と書けるので、\( n^m \)が現れるのは、下線を引いた
- \( \alpha_m n^m \)
- \( – \alpha_m (n-1)^m \)
の2ヶ所だけです。
ここの部分を計算してみると
\begin{align*}
& \alpha_m n^m – \alpha_m (n-1)^m \\
= & \alpha_m n^m – \alpha_m n^m – m\alpha_{m-1} n^{m-1} – \cdots \\
& – \cdots – m\alpha_1 n – \alpha_0 \\
= & – m\alpha_{m-1} n^{m-1} – \cdots – m\alpha_1 n – \alpha_0 \\
\end{align*}
となり、確かに\( n^m \)の項が消えます。
よって、nのm次式で表される数列についても、階差数列が(m-1)次式で表されるということが言えます。
さて、ここまで、m次式で表される数列の階差数列は、(m-1)次式で表される数列になるということを見てきました。
このことと、後に紹介する「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」を用いれば、「どのような数列を利用すれば、2乗の和、3乗の和、…を求めることができるか?」といったことがわかるようになります。
教科書などで紹介されている2乗の和、3乗の和の求め方でも、「どこからあの式が出てきたのか?」といったことがわかるようになります。
階差数列の和が求められるなら、元の数列の一般項が求められる
さらに紹介したいのは、
階差数列\( \{ b_n \} \)の和が求められるなら、元の数列\( \{ a_n \} \)の一般項が求められる
ということ。
このことは、ここから見ていくことの基本になりますので、しっかり身につけていきましょう。
まずは、具体的な数列として、初項から1,2,3,・・・と足していった数列
\[ a_n:1,2,4,7,11,16, \cdots \]
の第10項と第n項を求めてみます。
その後
数列\( \{ a_n \} \)の階差数列を\( \{ b_n \} \)とした場合、数列\( \{ a_n \} \)の第n項がどのように表せるのか
を見ていきます。
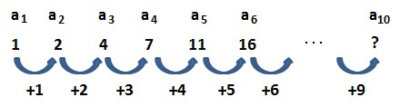
数列\( \{ a_n:1,2,4,7,11,16, \cdots \} \)の第10項を求める
まずは、1から始まり、順番に1,2,3,・・・と足していった数列
\[ a_n:1,2,4,7,11,16, \cdots \]
の数列の第10項を求めてみましょう。
以下の図のように、数列\( \{ a_n \} \)の変化していく様子を順番に考えてみましょう。
この図から考えていただきたいのは、等差数列や等比数列の一般項を考えたときと同じように
\( a_1 \)との関係性
です。
図を見てみると
\( a_2 \)は、\( a_1 \)に\( 1 \)を足した数
\( a_3 \)は、\( a_1 \)に\( 1 + 2 \)を足した数
\( a_4 \)は、\( a_1 \)に\( 1 + 2 + 3 \)を足した数
\( a_5 \)は、\( a_1 \)に\( 1 + 2 + 3 + 4 \)を足した数
となっています。
同じように考えていけば
\( a_{10} \)は、\( a_1 \)に\( 1 + 2 + 3 + \cdots + 9 \)を足した数
になることがわかります。
つまり
\begin{align*}
a_{10} = & a_1 + ( 1 + 2 + 3 + \cdots + 9 ) \\
= & 1 + \frac{1}{2}\cdot9\cdot10 \\
= & 1 + 45 \\
= & 46
\end{align*}
と計算することができ、\( a_{10} \)を求めることができました。
数列\( \{ a_n:1,2,4,7,11,16, \cdots \} \)の第n項を求める
では、第n項\( a_n \)はどのように表すことができるでしょうか。
第10項を求めたときと同じように
\( a_2 \)は、\( a_1 \)に\( 1 \)を足した数
\( a_3 \)は、\( a_1 \)に\( 1 + 2 \)を足した数
\( a_4 \)は、\( a_1 \)に\( 1 + 2 + 3 \)を足した数
\( a_5 \)は、\( a_1 \)に\( 1 + 2 + 3 + 4 \)を足した数
…
\( a_{10} \)は、\( a_1 \)に\( 1 + 2 + 3 + \cdots + 9 \)
…
と考えていくと
\( a_{n} \)は、\( a_1 \)に\( 1 + 2 + 3 + \cdots + (n-1) \)を足した数
であることがわかります。
つまり、いま考えている\( 1,2,4,7,11,16, \cdots \)という数列の一般項\( a_n \)は
\begin{align*}
a_n = & a_1 + \{ 1 + 2 + 3 + \cdots + (n-1) \} \\
= & 1 + \frac{1}{2}(n-1)n \\
\end{align*}
と表すことができるのです。
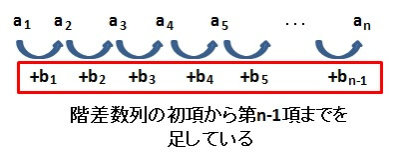
階差数列が\( \{ b_n \} \)となる数列\( \{ a_n \} \)の第n項を求める
もっと一般的に、数列\( \{ a_n \} \)の階差数列を\( \{ b_n \} \)とした場合を考えましょう。
ここまで見てきたように考えれば、
\( a_n \)は、初項\( a_1 \)に階差数列\( \{ b_n \} \)の初項から第n-1項までの和を足した数
といえます。
これを式にすると
\begin{align*}
a_n & = a_1 + (b_1 + b_2 + \cdots + b_{n-1}) \\
& = a_1 + \sum_{k=1}^{n-1} b_k
\end{align*}
と表すことができるのです。
最後に、ここまで見てきたことをまとめておきましょう。
数列\( \{ a_n \} \)の階差数列を\( \{ b_n \} \)としたとき、数列\( \{ a_n \} \)の一般項\( a_n \)は
\begin{align*}
a_n & = a_1 + (b_1 + b_2 + \cdots + b_{n-1}) \\
& = a_1 + \sum_{k=1}^{n-1} b_k \phantom{xxx} (n = 2,3,4,\cdots)
\end{align*}
と表すことができる
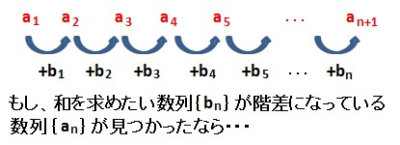
和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる
最後は、
和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる
ということです。
これは、すでに紹介した
階差数列\( \{ b_n \} \)の和が求められるなら、元の数列\( \{ a_n \} \)の一般項が求められる
ということを、逆に見ればわかります。
階差数列\( \{ b_n \} \)の和は、\( a_{n+1} – a_1 \)で計算できる
まず、和を求めたい数列を\( \{ b_n \} \)としましょう。
そのとき、\( \{ b_n \} \)が階差数列となるような数列\( \{ a_n \} \)を見つけることができたら、どうでしょうか?
言い換えるなら、
\[ b_n = a_{n+1} – a_n \]
となるような数列\( \{ a_n \} \)を見つけることができれば、数列\( \{ b_n \} \)の和はどのように計算できるでしょうか?
「階差数列の和を求めれば、元の数列の一般項を求められる」でも見たように、第n+1項は
\begin{align*}
a_{n+1} = a_1 + \sum_{k=1}^{n} b_k
\end{align*}
となっています。
この式を
\begin{align*}
\sum_{k=1}^{n} b_k = a_{n+1} – a_1
\end{align*}
と変形すると、”階差数列\( \{ b_n \} \)の和は、数列\( \{ a_n \} \)の第n+1項\( a_{n+1} \)から初項\( a_1 \)を引いたもの”になっています。
つまり、ここからわかることは
和を求めたい数列が階差数列となっているような数列を見つければ、数列の和は計算できる
ということです。
和を求めたい数列が階差数列になるような数列を見つけるには?
ここまでの説明を見てきて

でも、”和を求めたい数列が階差数列になるような数列を見つけろ”って言われても…
とお思いでしょう。
確かに、和を求めたい数列が階差となるような数列を見つけることは簡単ではありません。
しかし、すでに
公比\( r \)の等比数列の階差数列は、元の数列の\( (r-1) \)倍になる
m次式の数列の階差数列は、(m-1)次式の数列になる
ということを見てきました。
これは、逆に考えると
公比\( r \)の等比数列が階差数列となる数列は、階差数列の\( \frac{1}{r-1} \)倍の等比数列
m次式の数列が階差数列となる数列は、(m+1)次式の数列である
ということです。
つまり、いままで見てきたことを考えると
公比\( r \)の等比数列の和を求めたければ、その数列の\( \frac{1}{r-1} \)倍の等比数列を考えればいいのでは?
m次式の数列の和を求めたければ、(m+1)次式の数列を利用すればいいのでは?
ということが思いつきます。
言葉で説明しても、なかなかピンとこないと思います。
それぞれ
の中で、階差数列を利用して和を求めている箇所がありますので、参考にしてみてください。