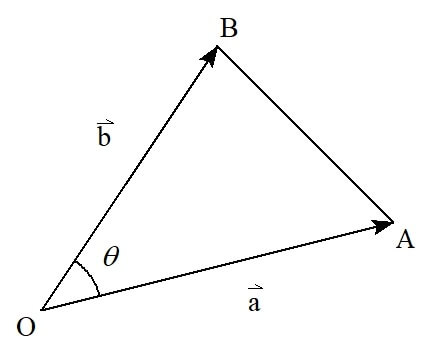
ここまで「ベクトルの基本事項」や「ベクトルの成分表示と演算」で、ベクトルの和や差・実数倍といった計算方法を見てきました。
「和や差があるのなら、積(掛け算)もあるの?」
と思われた方もいらっしゃると思います。
ベクトルには、掛け算に似た”内積”という演算があります。
ここでは、その内積を紹介します。
具体的には
- 内積の定義
- なぜ、内積はこのような定義なのか?
といったことを考えていきます。
内積の定義
いきなりですが、ここで紹介する”内積”は次のように定義されます。
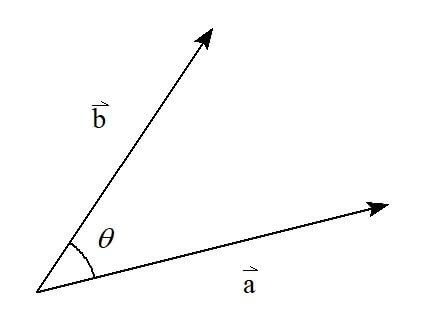
任意のベクトル\( \vec{a} , \vec{b} \)に対して、\( \vec{a} \)と\( \vec{b} \)のなす角を\( \theta \)とする。このとき、\( \vec{a} , \vec{b} \)の内積\( \vec{a} \cdot \vec{b} \)は
\[ \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos{\theta} \]
※ベクトルのなす角とは、下の図のように2つのベクトルの始点を合わせたときにできる角度のことです。
なぜ、内積はこのような定義なのか?
なぜ、ベクトルの内積はこのようなよくわからない定義なのか?
その理由としては、次の2つのメリットを得られるからです。
- ベクトルを成分表示したときに、内積はとても簡単な形で書くことができる
- 角度の代わりに内積を計算すれば済むようになる
メリット1:内積はとても簡単な形で表すことができる
まずひとつ目のメリットは、「成分表示したときに簡単な形で表すことができる」ということから見ていきましょう。
ここでポイントとなるのは”余弦定理”です。
(余弦定理については、正弦定理・余弦定理についてにて詳しく説明していますので、忘れてしまった方はこちらも参考にしてください。)
以下の図のように、2つのベクトル\( \vec{a} , \vec{b} \)の始点を合わせ、三角形\( \mathrm{OAB} \)を作ります。
このとき
\begin{align}
& \overrightarrow{\mathrm{OA}} = \vec{a} \\
& \overrightarrow{\mathrm{OB}} = \vec{b} \\
& \overrightarrow{\mathrm{AB}} = \vec{b} – \vec{a} \\
\end{align}
となります。
ここで、\( \vec{a} \)と\( \vec{b} \)のなす角を\( \theta \)とし、三角形\( \mathrm{OAB} \)に余弦定理を用いると
\begin{align}
& \mathrm{AB}^2 = \mathrm{OA}^2 + \mathrm{OB}^2 – 2\mathrm{OA} \cdot \mathrm{OB} \cos{\theta} \\
\Leftrightarrow \ & |\vec{b} – \vec{a}|^2 = |\vec{a}|^2 + |\vec{b}|^2 -2 \underline{ |\vec{a}||\vec{b}|\cos{\theta} } \\
\end{align}
と表すことができます。
このようにをベクトルを用いると、余弦定理の式の中に内積が隠れていることがわかります(下線部の部分です)。
よって、上記の式は
\[ |\vec{b} – \vec{a}|^2 = |\vec{a}|^2 + |\vec{b}|^2 -2 \vec{a} \cdot \vec{b} \]
と書き直すことができます。
ここで、2つのベクトル\( \vec{a} , \vec{b} \)が
\begin{align}
\vec{a} = (x_{1} ,y_{1}) \\
\vec{b} = (x_{2} ,y_{2}) \\
\end{align}
と成分表示されていたとすると、
\[ \vec{b} – \vec{a} = (x_{2} – x_{1} , y_{2} – y_{1} ) \]
と表せるので、それぞれのベクトルの大きさは
\begin{align}
& |\vec{a}|^2 = x_{1} {}^2 + y_{1} {}^2 \\
& |\vec{b}|^2 = x_{2} {}^2 + y_{2} {}^2 \\
& |\vec{b} – \vec{a}|^2 = ( x_{2} – x_{1} )^2 + ( y_{2} – y_{1} )^2 \\
\end{align}
これらの式を使って、余弦定理の式を変形していくと
\begin{align}
& |\vec{b} – \vec{a}|^2 = |\vec{a}|^2 + |\vec{b}|^2 -2 \vec{a} \cdot \vec{b} \\
\Leftrightarrow \ & ( x_{2} – x_{1} )^2 + ( y_{2} – y_{1} )^2 \\
& = x_{1} {}^2 + y_{1} {}^2 + x_{2} {}^2 + y_{2} {}^2 -2 \vec{a} \cdot \vec{b} \\
\Leftrightarrow \ & x_{2} {}^2 – 2 x_{1} x_{2} +x_{1} {}^2 + y_{2} {}^2 – 2 y_{1} y_{2} +y_{1} {}^2 \\
& = x_{1} {}^2 + y_{1} {}^2 + x_{2} {}^2 + y_{2} {}^2 -2 \vec{a} \cdot \vec{b} \\
\Leftrightarrow \ & – 2 ( x_{1} x_{2} + y_{1} y_{2} ) = -2 \vec{a} \cdot \vec{b} \\
\Leftrightarrow \ & \vec{a} \cdot \vec{b} = x_{1} x_{2} + y_{1} y_{2}
\end{align}
と表すことができます。
最後の式からわかるように、ベクトルの内積は
それぞれの成分どうしをかけて足したもの
になるのです。
\( \vec{a} = (x_{1} ,y_{1}) , \vec{b} = (x_{2} ,y_{2}) \)と成分表示したとき、ベクトルの内積は
\[ \vec{a} \cdot \vec{b} = x_{1} x_{2} + y_{1} y_{2} \]
と表すことができる。※このように表せるのは、余弦定理の式の中に内積が隠れているから
メリット2:角度の代わりに内積を計算すれば済むようになる
もう一つのメリットは「角度を計算する代わりに内積を計算すれば済むようになる」ということです。
代表的なもので言えば
- 垂直に交わるかどうかの判定
- 三角形の面積
のふたつ。
具体例1:垂直に交わるかどうかの判定
まずひとつ目の具体例は、「垂直に交わるかどうかの判定」です。
ここまで見てきたように、内積\( \vec{a} \cdot \vec{b} \)は
\begin{align}
& \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos{\theta} \\
& \vec{a} \cdot \vec{b} = x_{1} x_{2} + y_{1} y_{2} \\
\end{align}
という2つの表し方ができます。
ベクトルのなす角\( \theta = 90^{\circ} \)の場合、\( \cos{\theta} = 0 \)となります。
このとき、上の式から
\[ \vec{a} \cdot \vec{b} = 0 \]
この式と、下の式を合わせて考えると
\[ x_{1} x_{2} + y_{1} y_{2} = 0 \]
という式が導かれます。
つまり、垂直に交わることを証明したいなら
\( x_{1} x_{2} + y_{1} y_{2} = 0 \)を示せば良い
ということです。
内積を導入した結果、成分どうしのちょっとした計算をするだけで、垂直に交わっているかどうかを判断できるようになったのです。
具体例2:三角形の面積
次の具体例は「三角形の面積」です。
三角形の面積も、成分どうしの簡単な計算で求めることができるようになります。
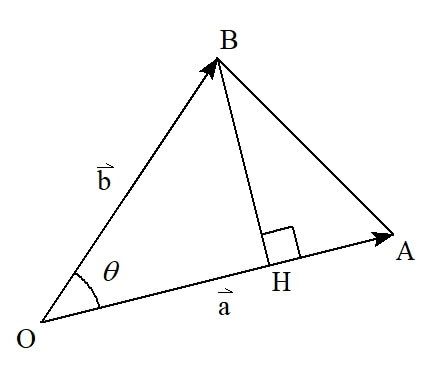
以下の図のように、三角形\( \mathrm{OAB} \)に対して、点\( \mathrm{B} \)から下ろした垂線の足を点\( \mathrm{H} \)、\( \angle \mathrm{AOB} = \theta \)とします。
この三角形\( \mathrm{OAB} \)の面積は
\begin{align}
& \frac{1}{2}|\overrightarrow{\mathrm{OA}} | |\overrightarrow{\mathrm{BH}} | \\
= & \frac{1}{2}|\overrightarrow{\mathrm{OA}} | |\overrightarrow{\mathrm{OB}} | \sin{\theta} \\
\end{align}
と表すことができます。
この式を内積\( \overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} \)を使って表すことができないか考えます。
内積の定義より、\( \overrightarrow{\mathrm{OA}} \)と\( \overrightarrow{\mathrm{OB}} \)の内積は
\[ \overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} = | \overrightarrow{\mathrm{OA}}| |\overrightarrow{\mathrm{OB}}| \cos{\theta} \]
と表せます。
しかし、ここまで見てきた三角形の面積の式には、\( \cos{\theta} \)がありません。代わりに\( \sin{\theta} \)が使われています。
そこで
\begin{align}
& \sin ^2 {\theta} + \cos ^2 {\theta} = 1 \\
\Leftrightarrow & \sin{\theta} = \sqrt{1 – \cos ^2 {\theta}}
\end{align}
という関係式を使って、三角形の面積の式を書き換えてみましょう。
\begin{align}
& \frac{1}{2}|\overrightarrow{\mathrm{OA}} | |\overrightarrow{\mathrm{OB}} | \sin{\theta} \\
= & \frac{1}{2}|\overrightarrow{\mathrm{OA}} | |\overrightarrow{\mathrm{OB}} | \sqrt{1 – \cos ^2 {\theta}} \\
= & \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2 |\overrightarrow{\mathrm{OB}}|^2 – |\overrightarrow{\mathrm{OA}}|^2 |\overrightarrow{\mathrm{OB}}|^2 \cos ^2 {\theta}} \\
= & \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2 |\overrightarrow{\mathrm{OB}}|^2 – (|\overrightarrow{\mathrm{OA}}| |\overrightarrow{\mathrm{OB}}| \cos{\theta} )^2 } \\
= & \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2 |\overrightarrow{\mathrm{OB}}|^2 – (\overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} )^2 } \\
\end{align}
ようやく内積を使って、三角形の面積を表すことができました。
ここで
\begin{align}
\overrightarrow{\mathrm{OA}} = ( x_{1} , y_{1} ) \\
\overrightarrow{\mathrm{OB}} = ( x_{2} , y_{2} ) \\
\end{align}
と成分表示されているとしましょう。
そうすると
\begin{align}
& |\overrightarrow{\mathrm{OA}}| = \sqrt{ x_{1} {}^2 + y_{1} {}^2 } \\
& |\overrightarrow{\mathrm{OB}}| = \sqrt{ x_{2} {}^2 + y_{2} {}^2 } \\
& \overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} = x_{1} x_{2} + y_{1} y_{2}
\end{align}
と表せます。
ですので、三角形の面積の式の\( \sqrt{\ \ } \)の中身は
\begin{align}
& |\overrightarrow{\mathrm{OA}}|^2 |\overrightarrow{\mathrm{OB}}|^2 – (\overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} )^2 \\
= & (x_{1} {}^2 + y_{1} {}^2)(x_{2} {}^2 + y_{2} {}^2) – (x_{1} x_{2} + y_{1} y_{2})^2 \\
= & x_{1} {}^2 x_{2} {}^2 + x_{1} {}^2 y_{2} {}^2 + y_{1} {}^2 x_{2} {}^2 + y_{1} {}^2 y_{2} {}^2 \\
& – (x_{1} {}^2 x_{2} {}^2 + 2 x_{1} x_{2} y_{1} y_{2} + y_{1} {}^2 y_{2} {}^2) \\
= & x_{1} {}^2 y_{2} {}^2 + y_{1} {}^2 x_{2} {}^2 – 2 x_{1} x_{2} y_{1} y_{2} \\
= & (x_{1} y_{2} – y_{1} x_{2})^2
\end{align}
となります。
よって、三角形の面積の式は、成分表示することによって
\begin{align}
& \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2 |\overrightarrow{\mathrm{OB}}|^2 – (\overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}} )^2 } \\
= & \frac{1}{2}\sqrt{ (x_{1} y_{2} – y_{1} x_{2})^2 } \\
= & \frac{1}{2} |x_{1} y_{2} – y_{1} x_{2}| \\
\end{align}
というシンプルな形で表現することができるのです。
このように、垂直のときと同じように、成分どうしのちょっとした計算で三角形の面積も求めることができるのです。
※この三角形の面積の公式は、公式を覚えるのではなく、導き方を理解するようにしてください。