ここでは、”n進法”という数字の表し方の説明をいたします。
まずは、わたしたちが普段使っている”十進法”
次に、コンピュータで取り入れられている”二進法”について考えていきます。
そして、”十進法”・”二進法”で考えたことを元に、”n進法の定義”について説明を行います。
また、参考書などではわかりにくい
- n進法から十進法への変換
- 十進法からn法への変換
が成り立つ理由も合わせて記載しています。
少しボリュームがありますが、少しずつ読み進めていただければ幸いです。
十進法について 普段の日常生活で使っている数の表し方

財布の中に、321円しか入ってなかった…。

今日の最高気温は、40.3度を記録しました。
これらの文章をみたとき”321”や”40.3”を”さんびゃくにじゅういち”、”よんじゅってんさん”と読みますよね。
誰も”さんにいいち”、”よんぜろてんさん”というふうには読みません。
これは、なぜでしょうか?
それは、わたしたちは、”十進法”という数の表し方のルールに従って、数字を解釈しているからです。
まずは、十進法の表し方のルールを、整数部分と少数部分に分けて確認していきましょう。
整数部分は、\( 1 \),\( 10 \),\( 100 \),…がそれぞれいくつあるか
まずは、十進法での整数の表し方を見ていきましょう。
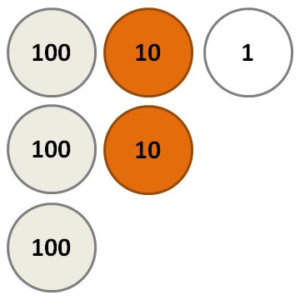
「財布の中に、321円しか入ってなかった…。」
この”321”という数字を見たとき、あなたの頭の中では、次のようなイメージが浮かび上がってきたのではないでしょうか。
【図:”321”のイメージ】
これを言葉で表現すると、
「”321″は、左から順番に
- 100が3個
- 10が2個
- 1が1個
ということを表している」となります。
あえて数式で表すと、以下の通りです。
\begin{align*}
321 & = 3 \times 100 + 2 \times 10 + 1 \\
& = 3 \times 10^2 + 2 \times 10^1 + 1 \times 10^0
\end{align*}
つまり、わたしたちが普段使っている”十進法”という数の表し方のルールで、整数を表す場合
…,\(10^p \),…,\( 10^2 \),\( 10^1 \),\( 10^0 \)がそれぞれいくつあるかを、\( 0 \)から\( 9 \)までの数字を並べて表現している
ということです。
少数部分は、\( 0.1 \),\( 0.01 \),\( 0.001 \),…がそれぞれいくつあるか
次に、少数の表し方を見ていきましょう。
考え方は、整数の場合と変わりません。
たとえば、“40.3”なら
- 10が4個
- 1が0個
- 0.1が3個
ということです。
これも、数式で表すと
\begin{align*}
40.3 & = 4 \times 10 + 0 \times 1 + 3 \times 0.1 \\
& = 4 \times 10^1 + 0 \times 10^0 + 3 \times 10^{-1}
\end{align*}
となります。
つまり、”十進法”で少数を含む数を表す場合
…,\( 10^p \),…,\( 10^2 \),\( 10^1 \),\( 10^0 \),\( 10^{-1} \),\( 10^{-2} \),…,\( 10^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 9 \)までの数字を並べて表現している
ということです。
十進法について、ここまで見てきたことをまとめておきましょう。
…,\(10^p \),…,\( 10^2 \),\( 10^1 \),\( 10^0 \),\( 10^{-1} \),\( 10^{-2} \),…,\( 10^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 9 \)までの10種類の数字を並べて表現する方法
二進法について コンピュータで使われている数の数え方
次は、”二進法”の表し方について。
コンピュータは、”電源のON・OFF”を利用して、”二進法”で数を数えています。
その二進法について、十進法のときと同じように、整数部分と少数部分に分けて説明していきます。
整数部分は、\( 2^0 \),\( 2^1 \),\( 2^2 \),…がそれぞれいくつあるか
これまで見てきたように、十進法で整数を表す場合
…,\( 10^p \),…,\( 10^2 \),\( 10^1 \),\( 10^0 \)がそれぞれいくつあるかを、\( 0 \)から\( 9 \)までの数字を左から順番に並べて表現する
ということを見てきました。
二進法についても、十進法と同じように考えます。
つまり、”二進法”で整数を表す場合
…,\( 2^p \),…,\( 2^2 \),\( 2^1 \),\( 2^0 \)がそれぞれいくつあるかを、\( 0 \)から\( 1 \)までの数字を並べて表現する
ということです。
たとえば、二進法で“10011”と表される数は
\begin{align*}
10011 = & \ 1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 \\
& + 1 \times 2^1 + 1 \times 2^0
\end{align*}
で計算される数である、ということです。
これを実際に計算すると
\[ 16 + 2 + 1 = 19 \]
となります。
つまり
二進法で”10011″と表される数は、十進法の”19″である
ということです。
少数部分は、\( 2^{-1} \),\( 2^{-2} \),\( 2^{-3} \),…がそれぞれいくつあるか
二進法の少数の表し方についても、十進法で見たのと同じように考えればいいのです。
つまり、”二進法”で、少数を含む数を表すには
…,\( 2^p \),…,\( 2^2 \),\( 2^1 \),\( 2^0 \),\( 2^{-1} \),\( 2^{-2} \),…,\( 2^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 1 \)までの数字を並べて表現する
ということです。
たとえば、二進法で“11.101”と表された数は
\begin{align*}
11.101 = & \ 1 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} \\
& + 0 \times 2^{-2} + 1 \times 2^{-3}
\end{align*}
で計算される数です。
計算すると
\begin{align*}
2 + 1 + \frac{1}{2} + \frac{1}{8} & = 2 + 0.5 + 0.125 \\
& = 3.625
\end{align*}
となりますので、
二進法で”11.101″と表される数は、十進法の”3.625″である
ということです。
二進法についても、ここでまとめておきましょう。
…,\( 2^p \),…,\( 2^2 \),\( 2^1 \),\( 2^0 \),\( 2^{-1} \),\( 2^{-2} \),…,\( 2^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 1 \)までの2種類の数字を並べて表現する方法
n進法の定義について
ここまで、十進法や二進法について見てきました。
n進法についても、同じように考えればOKです。
…,\( n^p \),…,\( n^2 \),\( n^1 \),\( n^0 \),\( n^{-1} \),\( n^{-2} \),…,\( n^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( n -1 \)までのn種類の数字を使って左から順番に並べて表現する方法
- n進法を十進法に変換する方法
- 十進法をn進法に変換する方法
について見ていきます。
n進法から十進法に変換する方法
まず、n進法を十進法に変換するのは、n進法の定義に従って計算すればいいだけです。
二進法から十進法への変換は、「二進法について」のところで、整数の場合と少数の場合とで2回やりました。
ここでは、三進法の数を十進法に直してみましょう。
(問題1)
三進法で”1201.1″と表された数を十進法で表せ。
(解説)
上記の【n進法とは】を見るとわかるように
三進法は
…,\( 3^p \),…,\( 3^2 \),\( 3^1 \),\( 3^0 \),\( 3^{-1} \),\( 3^{-2} \),…,\( 3^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 2 \)までの数を並べて表現する方法
です。
なので、三進法で”1201.1″と表された数は
\begin{align*}
1201.1 = & \ 1 \times 3^3 + 2 \times 3^2 + 0 \times 3^1 \\
& + 1 \times 3^0 + 1 \times 3^{-1}
\end{align*}
のことです。
これを計算すると
\[ 27 + 2 \cdot 9 + 1 + \frac{1}{3} = 46.333… \]
となります。
十進法からn進法に変換する方法
次に、十進法をn進法に変換する方法です。
ここでは
- 定義とにらめっこしながら計算する方法
- 参考書などによく載っている、割り算・掛け算を使った方法
の2通りの方法を、以下の問題を解きながら見ていきます。
(問題2)
十進法で”51.125″と表された数を四進法で表せ
方法1:定義とにらめっこしながら計算する
まず、【n進法とは】から、四進法の定義を確認しましょう。
四進法は
…,\( 4^p \),…,\( 4^2 \),\( 4^1 \),\( 4^0 \),\( 4^{-1} \),\( 4^{-2} \),…,\( 4^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 3 \)までを並べて表現する方法
です。
そして、十進法の”51.125″を四進法に変換するうえで、注意していただきたいポイントは2つ。
- \( 4^2 \)より大きい\( 4^3 \),\( 4^4 \),\( 4^5 \),…の係数は\( 0 \)である
- \( 4^2 \)の部分の係数は\( 0 \)ではない
ということ。
まず、ひとつ目の「\( 4^3 \),\( 4^4 \),\( 4^5 \),…の係数は\( 0 \)」について。
もし、\( 4^3 \),\( 4^4 \),\( 4^5 \),…の係数が\( 0 \)でないものがあれば、”51″より大きくなってしまいます。
これは、\( 4^3 \),\( 4^4 \),\( 4^5 \),…の係数が\( 0 \)でない数の中で、最も小さい\( 1 \times 4^3 \)を計算すると
\[ 1 \times 4^3 = 64 > 51 \]
となることからわかります。
ふたつ目の「\( 4^2 \)の部分の係数は\( 0 \)ではない」についても同様に考えられます。
いま、ひとつ目より\( 4^3 \),\( 4^4 \),\( 4^5 \),…の係数は\( 0 \)であることがわかっていますので、\( 4^2 \)の部分の係数も\( 0 \)であれば、整数部分は”51″よりも小さくなってしまいます。
これも、\( 4^2 \)以上の部分の係数が\( 0 \)の数の中で、最も大きい\( 3 \times 4^1 + 3 \times 4^0 \)を計算すると
\[ 3 \times 4^1 + 3 \times 4^0 = 15 < 51 \]
となるからです。
よって、上記の2つのポイントから
\begin{align*}
51.125 = & \ a \times 4^2 + b \times 4^1 + c \times 4^0 \\
& + d \times 4 ^{-1} + e \times 4 ^{-2} + \cdots
\end{align*}
と表されます。(ただし、\( a > 0 \))
ここからは、\( a \),\( b \),\( c \),\( d \),\( e \),…を順番に求めていきます。
まずは、いちばん大きくなる\( 4^2 \)の係数の\( a \)について。
四進法の定義を見るとわかるように、係数の部分には4より大きい数字が現れることはありません。
さらに、\( a > 0 \)なので、\( 1 \leq a \leq 3\)。
ここで
\begin{align*}
& 48 < 51 < 64 \\
\Leftrightarrow \ & 3 \times 4^2 < 51 < 4 \times 4^2
\end{align*}
であるから、\( a = 3 \)ということがわかります。
ここから、
\begin{align*}
51.125 = & \ 3 \times 4^2 + b \times 4^1 + c \times 4^0 \\
& + d \times 4^{-1} + e \times 4^{-2} + \cdots \\
\Leftrightarrow \ 3.625 = & \ b \times 4^1 + c \times 4^0 \\
& + d \times 4^{-1} + e \times 4^{-2} + \cdots
\end{align*}
と変形できます。
さらに\( b \)についても、\( a \)と同じように考えていくと
\begin{align*}
& 0 < 3 < 4 \\
\Leftrightarrow \ & 0 \times 4^1 < 3 < 1 \times 4^1
\end{align*}
となるので
\[ b = 0 \]
そして、
\begin{align*}
3.125 = & \ 0 \times 4^1 + c \times 4^0 \\
& \ + d \times 4 ^{-1} + \cdots \\
\Leftrightarrow \ 3.125 = & \ c \times 4^0 + d \times 4 ^{-1} + \cdots
\end{align*}
なので
\[ c = 3 \]
となります。
これで整数部分は四進数で\( 303 \)と表されることがわかりました。
残りの少数部分の”0.125”でも、同様に考えていきましょう。
\begin{align*}
4 ^{-1} & = \frac{1}{4} \\
& = 0.25
\end{align*}
なので、
\[ d = 0 \]
\begin{align*}
4 ^{-2} & = \frac{1}{16} \\
& = 0.0625
\end{align*}
であり
\[ 0.125 = 2 \times 0.0625 \]
と表せるので
\[ e = 2 \]
となり、小数部分は”0.02″と表されることがわかりました。
以上より、十進法で”51.125″と表された数は
\begin{align*}
51.125 = & \ 3 \times 4^2 + 0 \times 4^1 + 3 \times 4^0 \\
& \ + 0 \times 4 ^{-1} + 2 \times 4 ^{-2}
\end{align*}
と表すことができます。
つまり、十進法で”51.125″は、四進法では”303.02″と表される、ということです。
方法2:整数部分を割り算・少数部分は掛け算
参考書などには、”割り算や掛け算を使った方法”がよく載っています。
その方法は知っていても

そのやり方で、なぜn進法に変換できるのかわからない…
という方もいらっしゃると思います。
そこで、まずは(問題2)を参考書などによく載っている方法で解いてみます。
その後、”なぜ割り算や掛け算をすると変換できるのか”について見ていきます。
ここで、もう一度(問題2)を掲載しておきます。
(問題2)
十進法で”51.125″と表された数を四進法で表せ
(解答)
参考書によく載っている方法は、以下のような解き方です。
※解答を見ただけでは、”なぜn進法に変換できるのか?”がわかりにくいと思うで、まずは流れだけを意識して解答をご覧ください。
まずは、整数部分について。
整数部分は、四進数の基準に使う”4”で繰り返し割り算を行うと求められる。(理由は後述)
具体的にいうと、商が0になるまで整数部分を4で割り続け、
- ”4”で1回割ったときの余りが\( 4^0 \)の位
- ”4”で2回割ったときの余りが\( 4^1 \)の位
- ”4”で3回割ったときの余りが\( 4^2 \)の位
︙
という流れで求めることができるのです。
実際に、整数部分の”51”について、割り算を繰り返すと
\begin{align*}
& 51 \div 4 = 12 \cdots \underline{3} \\
& 12 \div 4 = \phantom{1} 3 \cdots \underline{0} \\
& \phantom{1} 3 \div 4 = \phantom{1} 0 \cdots \underline{3}
\end{align*}
となるので
- ”4”で1回割ったときの余り \( \underline{3} \) が\( 4^0 \)の位
- ”4”で2回割ったときの余り \( \underline{0} \) が\( 4^1 \)の位
- ”4”で3回割ったときの余り \( \underline{3} \) が\( 4^2 \)の位
になります。
つまり、整数部分の”51”は、四進数では”303″と表される。
次は、少数部分。
小数部分は、”4”で繰り返し掛け算を行うと求められる。(こちらも理由は後述)
具体的にいうと、小数部分が表れなくなるまで、小数部分の”0.125″に次々と4を掛けていく。
そのとき
- ”4”を1回掛けたときに現れる整数が\( 4^{-1} \)の位
- ”4”を2回掛けたときに現れる整数が\( 4^{-2} \)の位
- ”4”を3回掛けたときに現れる整数が\( 4^{-3} \)の位
︙
という流れで求めることができるということです。
実際に、小数部分の”0.125″について、少数部分が0になるまで4を掛けていくと
\begin{align*}
& 0.125 \times 4 = \underline{0}.5 \\
& \phantom{11} 0.5 \times 4 = \underline{2}.0
\end{align*}
となるので、
- ”4”で1回掛けたときの整数部分 \( \underline{0} \) が\( 4^{-1} \)の位
- ”4”で2回掛けたときの整数部分 \( \underline{2} \) が\( 4^{-2} \)の位
になります。
つまり、小数部分の”0.125″は、四進法では”0.02″と表される。
以上より、十進法で”51.125″と表された数は、四進法では”303.02″と表される。
割り算をすると整数部分が求められる理由
ここからは、”なぜ割り算で整数部分が求められるのか?”という理由について説明していきます。
いま、整数部分の”51″は、
\begin{align*}
51 = 3 \times 4^2 + 0 \times 4^1 + 3 \times 4^0
\end{align*}
と表されるということを見てきました。
この形にすることが、”なぜ割り算で整数部分が求められるのか?”を理解するために必要になってきます。
さらに、”4で割り切れる部分とそうでない部分に分ける”ということを行うと、よりわかりやすくなります。
\begin{align*}
& 3 \times 4^2 + 0 \times 4^1 + 3 \times 4^0 \\
= & \underline{ 4 (3 \times 4^1 + 0 \times 4^0) } + 3 \times 4^0
\end{align*}
と書き直してみる。
すると、下線部は4で割り切れ、残りの部分は4では割り切れないことがわかります。
つまり、割り算を1回行うと、\( 3 \times 4^0 \)の部分が余りとして出てくるということです。
さて、2回目の割り算を行っていきましょう。
今回、4で割っていくのは、1回目の割り算で割り切れた
\[ 12 = 3 \times 4^1 + 0 \times 4^0 \]
の部分になります。
1回目と同じように、4で割り切れる部分とそうでない部分に分けると
\begin{align*}
& 3 \times 4^1 + 0 \times 4^0 \\
= & \underline{4 (3 \times 4^0) } + 0 \times 4^0
\end{align*}
と書けます。
そして、1回目と同じように考えると、\( 0 \)が余りとして出てくるということがわかります。
つまり、割り算を2回行うと、\( 4^1 \)の位の\( 0 \)が余りとして出てくるのです。
そして、3回目の割り算です。
3回目では、
\[ 3 \times 4^0 \]
を4で割っていきますので、余りには
\[ 3 \]
がそのまま出てきます。
ここまで見てきたことをまとめておきます。
\[ 51 = 3 \times 4^2 + 0 \times 4^1 + 3 \times 4^0 \]
と書けるので、”51″を4で繰り返し割っていくと
- 1回目の割り算をしたとき、\( 4^2 \),\( 4^1 \)の部分は4で割り切れる
→\( 4^0 \)の係数 \( 3 \)が余りとして出てくる - 2回目の割り算をしたとき、\( 4^2 \)の部分は4で割り切れる
→\( 4^1 \)の係数 \( 0 \)が余りとして出てくる - 3回目の割り算をしたとき、4で割り切れる部分がない
→\( 4^2 \)の係数 \( 3 \)が余りとして出てくる
ということになります。
したがって、4で繰り返し割っていくと、整数部分をn進法に変換できるということです。
※ここで紹介した、”都合のいい部分とそうでない部分に分ける”という考え方は、ユークリッドの互除法や不定方程式でも使っています。合わせて見ていただくと、理解が深まります。)
掛け算をすると少数部分が求められる理由
次に、”なぜ掛け算で少数部分が求められるのか?”という理由を見ていきます。
小数部分の”0.125”についても
\begin{align*}
0.125 = 0 \times 4^{-1} + 2 \times 4^{-2}
\end{align*}
という表し方をすることで、”なぜ掛け算で少数部分が求められるのか?”がわかります。
それでは、実際に\( 0 \times 4^{-1} + 2 \times 4^{-2} \)に4を掛けていきます。
まず、4を1回掛けてみると
\begin{align*}
& (0 \times 4^{-1} + 2 \times 4^{-2}) \times 4 \\
= & 0 \times 4^0 + 2 \times 4^{-1}
\end{align*}
となり、\( 4^{-1} \)の係数\( 0 \)が整数部分に上がってくることがわかります。
そして、残りの少数部分の\( 2 \times 4^{-1} \)についても、4をもう一度掛けることで
\begin{align*}
& ( 2 \times 4^{-1}) \times 4 \\
= & 2 \times 4^0
\end{align*}
となり、整数部分に上がってきます。
まとめると、0.125は
\[ 0.125 = 0 \times 4^{-1} + 2 \times 4^{-2} \]
と書けるので、4を繰り返し掛けていくと
- 1回目の掛け算をしたとき、\( 4^{-1} \)の係数 \( 0 \)が整数部分に上がってくる
- 2回目の掛け算をしたとき、\( 4^{-2} \)の係数 \( 0 \)が整数部分に上がってくる
ということになります。
よって、4で繰り返し掛けていくと、少数部分をn進法に変換できるということです。
これらの方法は、四進法以外でも使えますので、他の進法でも計算してみてください。
十六進法について 数字以外の文字も使った数の表し方
最後に、”十六進法”について説明いたします。
十六進法についても、【n進法とは】で紹介した定義に当てはめて考えてみましょう。
十六進法とは
…,\( 16^p \),…,\( 16^2 \),\( 16^1 \),\( 16^0 \),\( 16^{-1} \),\( 16^{-2} \),…,\( 16^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 15 \)までの16種類の数字を使って左から順番に並べて表現する方法
しかし、この”十六進法の定義?”には、ひとつ欠点があるのです。
それは、”2通りに解釈できてしまう数がある”ということです。
そのことを体験するためにも、次の問題を一度考えて見てください。
(問題3)
十六進法で”124”と表された数を十進法で表わせ
(解説)
[解答A]
十六進法で”124″と表されているので
- \( 16^2 \)の係数…\( 1 \)
- \( 16^1 \)の係数…\( 2 \)
- \( 16^0 \)の係数…\( 4 \)
と解釈できる。
よって、
\begin{align*}
& 1 \times 16^2 + 2 \times 16^1 + 4 \times 16^0 \\
= & 256 + 2 \cdot 16 + 4 \\
= & 256 + 32 + 4 \\
= & 292
\end{align*}
[解答B]
十六進法で”124″と表されているので
- \( 16^1 \)の係数…\( 12 \)
- \( 16^0 \)の係数…\( 4 \)
と解釈できる。
よって、
\begin{align*}
& 12 \times 16^1 + 4 \times 16^0 \\
= & 12 \cdot 16 + 4 \\
= & 192 + 4 \\
= & 196
\end{align*}
このように、”124”が2通りに解釈できてしまうのは、”12″の部分が原因です。
具体的にいうと、わたしたちが普段使っている数字が\( 0 \)~\( 9 \)までの10種類しかないので、10以上の数を1文字で表すことができないことが原因です。
つまり、2通りに解釈できないようにするには、\( 10 \)~\( 15 \)の数を、それぞれ数字以外の1文字で表現しなければならないということです。
そこで、十六進法では
- \( 10 \)は\( \rm{A} \)
- \( 11 \)は\( \rm{B} \)
- \( 12 \)は\( \rm{C} \)
- \( 13 \)は\( \rm{D} \)
- \( 14 \)は\( \rm{E} \)
- \( 15 \)は\( \rm{F} \)
を使って、1文字で表現します。
正しい十六進法の定義は、以下のようになります。
…,\( 16^p \),…,\( 16^2 \),\( 16^1 \),\( 16^0 \),\( 16^{-1} \),\( 16^{-2} \),…,\( 16^{-q} \),…がそれぞれいくつあるかを、\( 0 \)から\( 9 \),AからFの16種類の文字を使って左から順番に並べて表現する方法
※ただし、\( \rm{A} \)は\( 10 \)、\( \rm{B} \)は\( 11 \)、\( \rm{C} \)は\( 12 \)、\( \rm{D} \)は\( 13 \)、\( \rm{E} \)は\( 14 \)、\( \rm{F} \)は\( 15 \)として扱う。
このように定義することで、2通りに解釈できるという欠点が解消されました。
もう一度(問題3)を見ていきましょう。
”124”は
- \( 16^2 \)の係数…\( 1 \)
- \( 16^1 \)の係数…\( 2 \)
- \( 16^0 \)の係数…\( 4 \)
という1通りの解釈に決まることになります。
よって、十六進法の”124″を十進法で表すと
\[ 292 \]
ちなみに、十進法の”196″は、十六進法では
- \( 16^1 \)の係数…\( 12 = \rm{C} \)
- \( 16^0 \)の係数…\( 4 \)
であるので
\[ \rm{C}4 \]
と表されます。