「ベクトルの基本事項」の中で、
- ベクトルの和や実数倍
- ベクトルの成分表示
について学びました。
ここでは、
- 成分表示されたベクトルの和や実数倍がどのように計算することができるのか
ということを見ていきます。
ベクトルの成分表示(復習)
ベクトルの成分表示とは、座標を使って
\( x \)軸方向・\( y \)軸方向にいくつ進んだか
でベクトルを表現する方法でした。
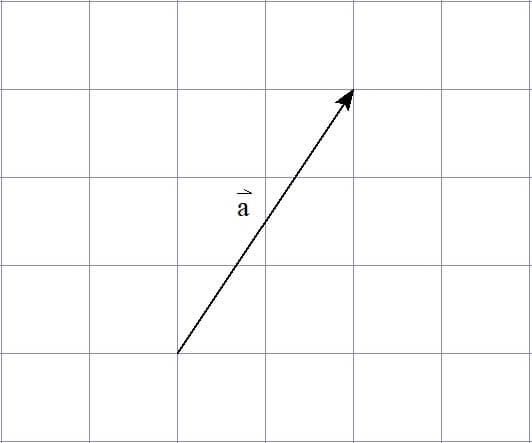
次の図の場合、ベクトル\( \vec{a} \)は、
\( x \)軸方向に2、\( y \)軸方向に3進んだベクトル
ということができます。
このとき、ベクトル\( \vec{a} \)を
\[ \vec{a} = (2,3) \]
と表すのがベクトルの成分表示でした。
成分表示されたベクトルの演算
ここから、ベクトルの和や実数倍について、どのように計算することができるのかを見ていきます。
ここでは、成分表示されたベクトルの例として
\begin{align}
\vec{a} = (2,3) \\
\vec{b} = (4,1) \\
\end{align}
を使って、ベクトルの実数倍や和(足し算)、差(引き算)がどうなるのかを見ていきましょう。
実数倍(2倍、3倍…)
まずは、ベクトルの実数倍です。
「ベクトルの基本事項」でも説明したように、ベクトルの実数倍は
ベクトルの拡大・縮小
でした。
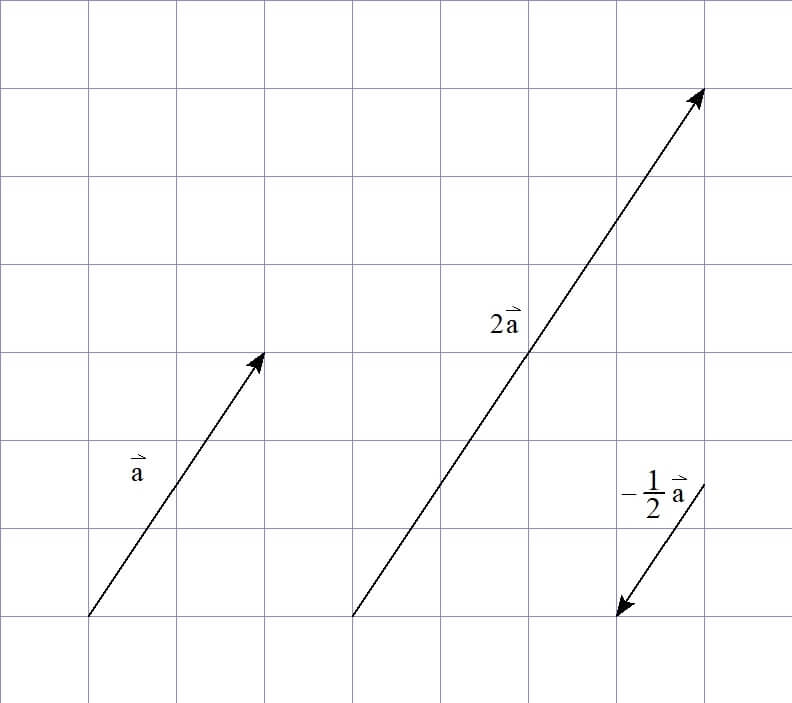
ここでは、\( 2\vec{a} \)がどのような成分表示になるか考えてみましょう。
\( 2\vec{a} \)は、\( \vec{a} \)と比べて長さが2倍になっています。
当然、\( x \)軸方向にも2倍進んでいます。\( y \)軸方向も同様です。
つまり、\( 2\vec{a} \)は
\begin{align}
2\vec{a} & = 2(2,3) \\
& = (2 \times 2 ,2 \times 3) \\
& = (4,6) \\
\end{align}
と計算することができます。
このように、成分表示されたベクトルの実数倍(2倍、3倍…)は
各成分を2倍、3倍…したもの
になります。
和(足し算)
次は、ベクトルの和(足し算)です。
「ベクトルの基本事項」でも説明したように、ベクトルの和(足し算)は
ベクトルの継ぎ足し
でした。
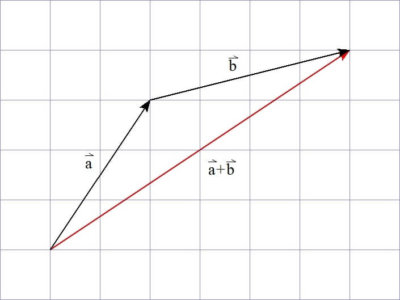
さて、ベクトルの和\( \vec{a} + \vec{b} \)は、どのような成分表示になるでしょうか。
まずは、\( x \)成分について
図を見ると明らかですが、ベクトル\( \vec{a} \)で2、ベクトル\( \vec{b} \)で4だけ\( x \)軸方向に進んでいますので、 ベクトル\( \vec{a} + \vec{b} \)では合計6進んでいます。
同様に、\( y \)成分についても、ベクトル\( \vec{a}, \vec{b} \)でそれぞれ3、1ずつ進みますので、合計で4。
つまり、\( \vec{a} + \vec{b} \)は
\begin{align}
\vec{a} + \vec{b} & = (2,3) + (4,1) \\
& = (2+4 ,3+1) \\
& = (6,4)
\end{align}
と計算することができます。
このように、成分表示されたベクトルの和(足し算)は
同じ成分どうしを足したもの
になります。
差(引き算)
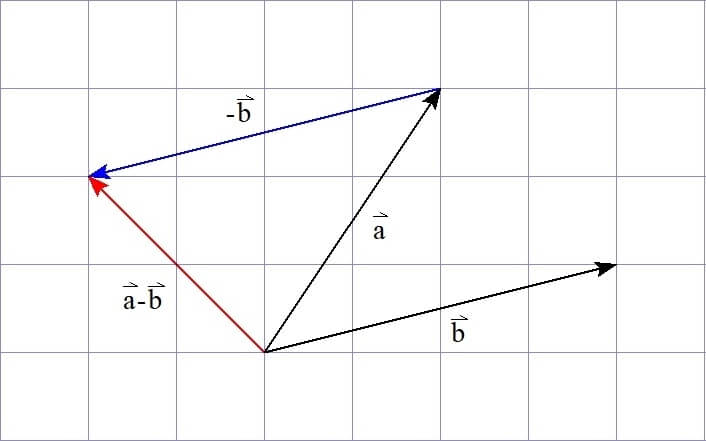
ベクトルの差についてはどうでしょうか。
ベクトルの差(引き算)は、「ベクトルの基本事項」で
逆ベクトルを足したもの
と説明しました。
ベクトル\( \vec{b} \)の逆ベクトル\( -\vec{b} \)は、ベクトル\( \vec{b} \)に-1をかけたものですので
\begin{align}
-\vec{b} & = -(4,1) \\
& = (-4,-1) \\
\end{align}
となります。
つまり、\( \vec{a} – \vec{b} \)は
\begin{align}
\vec{a} – \vec{b} & = (2,3) – (4,1) \\
& = (2,3) + (-4,-1) \\
& = (2-4 ,3-1) \\
& = (-2,2)
\end{align}
と計算することができます。
このように、成分表示されたベクトルの差(引き算)は
同じ成分どうしで引いたもの
になります。