三角形の”合同条件・相似条件”の意味についてのところで述べたように、三角形の辺・角度のうちのいくつかが与えられれば三角形の形や大きさがただ１通りに決まります。
では、三角形の形や大きさが１通りに決まったとき、与えられた以外の辺の長さや角度を求めることができないでしょうか？
それは、ここで学ぶ”正弦定理・余弦定理”を用いれば可能になります。
この２つの定理は高校数学の中でも、最も重要な定理のひとつです。
まずは、これらの定理を適切に使えるようになることが何よりも大切です。
問題演習を繰り返し、体に染み込ませていきましょう。
正弦定理・余弦定理とは？
まずは、”正弦定理・余弦定理”がどのような定理なのかを紹介します。
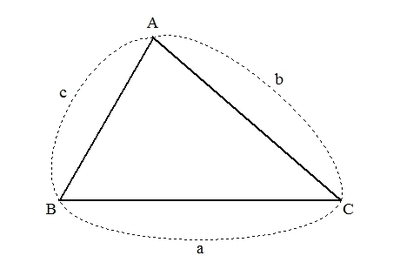
以下のような三角形ABCについて、次の式が成り立つ。（ただし、\( R \)は外接円の半径とする。）
\[ \frac{a}{\sin A} = \frac{b}{\sin B} =\frac{c}{\sin C} = 2R \]
以下のような三角形ABCについて、次の式が成り立つ。
\begin{align*}
a^2 = b^2 + c^2 -2bc \cos A
\end{align*}
これらの式を見るとわかるように、正弦定理・余弦定理は”辺の長さや角の大きさを求める定理”だと言えます。
高校数学においては、まずは正弦定理・余弦定理を適切に使えるようになることが、何よりも大切です。
なので、数学が苦手な方や時間に余裕のない方は、証明や導き方を後回しにしていただいても構いません。（本音を言うと、自力で証明できない定理・公式は使ってほしくないのですが…）
※証明に関しては、別ページにて解説予定です。
以下では、正弦定理・余弦定理を使うときはいつなのか、使える条件は何なのか、といったことを説明していきます。
正弦定理・余弦定理の使い方 それぞれを使い分けよう
では、まずは、どのような場合に正弦定理を使うのか、余弦定理を使うのかを見ていきます。
正弦定理・余弦定理は、それぞれ以下のような式でした。
【正弦定理】
\[ \frac{a}{\sin A} = \frac{b}{\sin B} \]
【余弦定理】
\[ c^2 = a^2 + b^2 -2ab \cos C \]
これを見てわかることは
- 正弦定理には、辺が２つ、角が２つ現れている
- 余弦定理には、辺が３つ、角が１つ現れている
ということです。
このことから
- 辺が３つ与えられたとき
…余弦定理を使うことができ、角の大きさが求められる - 辺が２つ、角が１つ与えられたとき
…正弦定理・余弦定理の両方を使うことができる
正弦定理を使えば、角の大きさが求められる
余弦定理を使えば、辺の長さが求められる - 辺が１つ、角が２つ与えられたとき
…正弦定理を使うことができ、辺の長さを求めることができる
ということがわかります。
いくつか問題を解いていきましょう。
問題１：辺が２つ、角が１つ与えられたとき
（問題１）
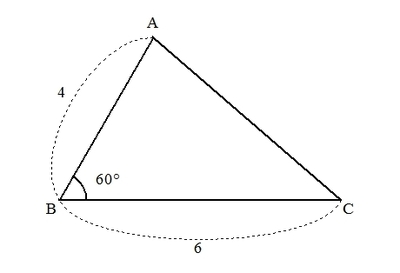
三角形ABCにおいて、辺AB=\( 4 \)、辺BC=\( 6 \)、∠ABC=\( 60^\circ \)とする。このとき、辺ACの長さを求めよ
（解説）
いま、条件として、辺が２つ、角が１つ与えられています。
なので、辺ACを求めるために、余弦定理を用いると
\begin{align*}
AC^2 & = AB^2 + BC^2 -2 \cdot AB \cdot BC \cos B \\
& = 4^2 + 6^2 -2 \cdot 4 \cdot 6 \cos 60^\circ \\
& = 16 + 36 -48 \cdot \frac{1}{2} \\
& = 28
\end{align*}
辺の長さは\( 0 \)より大きいので、
\[ AC = 2 \sqrt{7} \]
問題２：辺が１つ、角が２つ与えられたとき
（問題２）
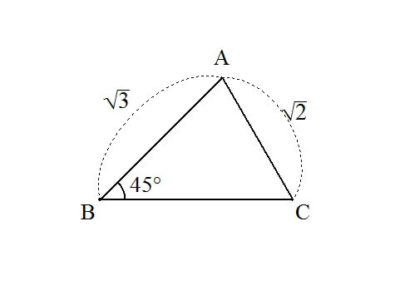
三角形ABCにおいて、辺AB=\( \sqrt{3} \)、辺AC=\( \sqrt{2} \)、∠ABC=\( 45^\circ \)とする。このとき、∠ACBを求めよ
（解説）
まず、∠ABC=\( 45^\circ \)であるから、∠ACBの取りうる値の範囲は
\[ 0^\circ < ∠ACB < 135^\circ \]
いま、条件として、辺が２つ、角が１つ与えられています。
なので、∠ACBを求めるために、正弦定理を用いると
\begin{align*}
& \frac{AB}{\sin C} = \frac{AC}{\sin B} \\
\Leftrightarrow \ & \frac{\sqrt{3}}{\sin C} = \frac{\sqrt{2}}{\sin 45^\circ} \\
\Leftrightarrow \ & \frac{\sqrt{3}}{\sin C} = \frac{\sqrt{2}}{\frac{1}{\sqrt{2}}}
\end{align*}
となります。
よって
\begin{align*}
\sin C & = \sqrt{3} \cdot \frac{1}{\sqrt{2}} \cdot \sin 45^\circ \\
& = \sqrt{3} \cdot \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\
& = \frac{\sqrt{3}}{2}
\end{align*}
つまり、
\[ ∠ACB = 60^\circ \verb|または| ∠ACB = 120^\circ \]
であることがわかります。
※２つとも、\( 0^\circ < ∠ACB < 135^\circ \)を満たすので、解として適切です。
※三角比の定義を、単位円を用いて拡張したため、鈍角であっても値を求めることができるのです。(拡張するメリットのひとつです。)
(三角比に関しては、三角比とは？定義の意味やポイントで詳しく説明していますので、合わせてご覧ください。)
正弦定理・余弦定理のポイントは、”使った条件で大きさ・形が決まるか？”
問題１では、答えがただ１つだけ出てきました。
しかし、問題２では、答えが２つ出てきました。
この違いはなんでしょうか？
答えは、”三角形の辺の長さ・角の大きさがただ１通り決まるかどうか”です。
”三角形の辺の長さ・角の大きさがただ１通り決まる条件”については、三角形の”合同条件・相似条件”の意味についてで説明しました。
それは、以下のような条件でした。
【三角形の辺の長さ・角の大きさがただ１通り決まる条件】
- ３辺の長さが与えられたとき
- ２辺の長さとその間の角が与えられたとき
- １辺の長さとその両端の角が与えられたとき
こういった条件を与えられたとき、”正弦定理・余弦定理”を使うと、辺の長さや角の大きさがただ１通りに求めることができます。
大きさ・形がただ１通りに決まっているとき、”正弦定理・余弦定理”を適切に使えば、各辺の長さや角の大きさをただ１通りに求めることができるということです。
ポイントになるのは、”使った条件で大きさ・形がただ１通り決まるか？”ということです。
たとえ、三角形がただ１通りに決まっていても、正弦定理・余弦定理に使用した条件では三角形がただ１つに決まらない場合、答えが複数出てくることがあります。
そのことを、次の問題を通じて見ていきましょう。
問題３：余弦定理を使ったとき、解が２つ出てくるのはなぜ？
（問題３）
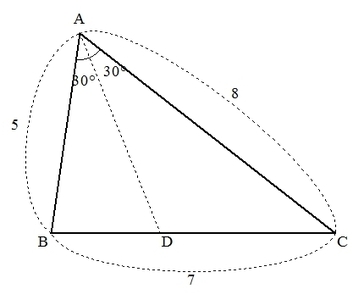
三角形ABCにおいて、AB=\( 5 \),AC=\( 8 \),BC=\( 7 \),∠BAC=\( 60^\circ \)とし、∠BACの二等分線と辺BCとの交点をDとする。
このとき、辺ADの長さを求めよ。
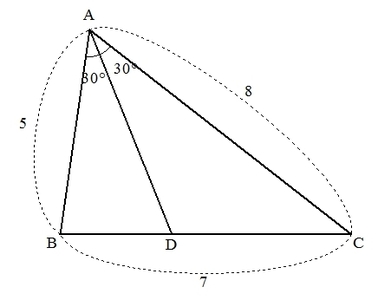
（解説）
まず、中学の復習になりますが、角の二等分線の定理を紹介します。
三角形ABCの∠Aの二等分線と辺BCとの交点をDとすると、
\[ BD:DC = AB:AC \]
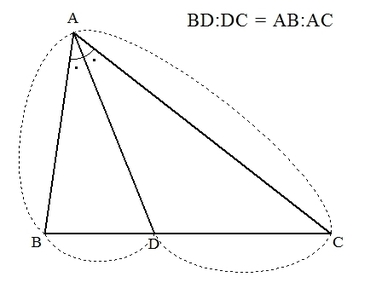
角の二等分線の定理より
\[ BD:DB = 5:8 \]
なので
\begin{align*}
BD &= \frac{5}{13} BC \\
&= \frac{35}{13}
\end{align*}
であることがわかります。
ここからは、よくある誤答をひとつ紹介します。
どこが間違っているか、考えてみてください。
（誤答例）
三角形ABDに着目し、余弦定理を使うと、
\begin{align*}
&(\frac{35}{13})^2 = 5^2 + AD^2 – 2 \cdot 5 \cdot AD \cos 30^\circ \\
\Leftrightarrow \ & AD^2 -5\sqrt{3}AD + \frac{3000}{169} = 0 \\
\Leftrightarrow \ & (AD – \frac{5 \sqrt{3} }{2} )^2 -\frac{75}{4} + \frac{3000}{169} = 0 \\
\Leftrightarrow \ & (AD – \frac{5 \sqrt{3} }{2} )^2 = \frac{675}{169 \cdot 4} \\
\Leftrightarrow \ & AD = \frac{5 \sqrt{3} }{2} \pm \frac{15 \sqrt{3} }{13 \cdot 2} \\
& \phantom{AD} = \frac{25\sqrt{3}}{13},\frac{40\sqrt{3}}{13}
\end{align*}
よって、辺ADの長さは
\[ \frac{25\sqrt{3}}{13} \ \text{または} \ \frac{40\sqrt{3}}{13} \]
上記の誤答例のどこがおかしいのでしょうか。
それは、三角形ABDはただ１通りに決まるのに、ADの長さが２通り存在すると解答している点です。
まず、三角形ABCですが、３辺が与えられているので、三角形の大きさ・形がただ１通りに決まります。そのため、∠ABCの角度もただ１通りしかありえません。
次に三角形ABDですが、条件から辺AB、辺BDの値が求められます。
いま、三角形ABCによって、∠ABCの角度もただ１通りに決まりますから、２辺とその間の角（辺AB、辺BD、∠B）の条件が与えられた状態になっています。
つまり、三角形の辺の長さ・角の大きさがただ１通り決まる条件を満たしているため、三角形ABDの辺の長さ・角の大きさもただ１通りに決まるはずです。
では、なぜ誤答例では辺の長さが２通り出てきたのでしょうか？
それは、余弦定理を用いた際に使った条件では三角形が１通りに決まらないためです。
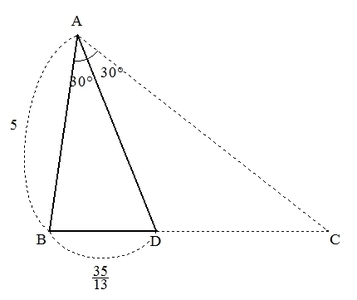
誤答例では、余弦定理で計算するにあたって、辺AB=\( 5 \)、辺BD=\( \displaystyle \frac{35}{13} \)、∠A=\( 30^\circ \)の条件を用いました。
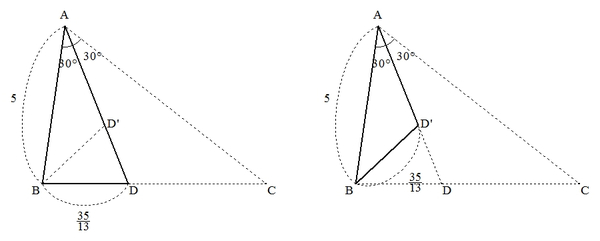
しかし、この条件を満たす三角形は、以下の図で表すように２通り存在します。
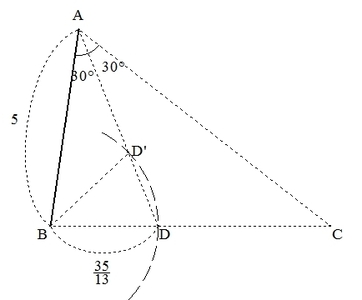
このように、条件を適切に与えないと、適切でない答えがでてきてしまうことがありうるのです。
それでは、解答に戻り、正しい答えを導いていきましょう。
（解説 続き）
まず、三角形ABDを１通りに定めるために∠Bに関する条件を求めます。
そこで、三角形ABCに着目し、\( \cos B \)を求めます。
余弦定理より
\begin{align*}
&8^2 = 5^2 + 7^2 – 2 \cdot 5 \cdot 7 \cos B \\
\Leftrightarrow \ &70 \cos B = 10 \\
\Leftrightarrow \ &\cos B = \frac{1}{7}
\end{align*}
次に、三角形ABDに着目して、余弦定理より
\begin{align*}
AD^2 &= 5^2 + (\frac{35}{13})^2 -2 \cdot 5 \cdot \frac{35}{13} \cos B \\
&= 25 + \frac{1225}{169} – \frac{50}{13} \\
&= \frac{4800}{169} \\
&= \frac{2^6 \cdot 3 \cdot 5^2}{13^2} \\
AD &= \frac{2^3 \cdot 5 \sqrt{3} }{13} \\
&= \frac{40 \sqrt{3} }{13}
\end{align*}