ここでは
\[ 1 + 2 + 3 + \cdots + n \]
といった自然数の和を扱います。
ここで紹介する1からnまでの和の公式は、以下のようになります。
\begin{align*}
& 1 + 2 + 3 + \cdots + n \\
= & \frac{1}{2}n(n+1)
\end{align*}
この公式を、いろんな方法で導いていきます。
大きく分けると
- 図形を用いる方法
- 階差数列を利用する方法
のふたつあり、それぞれいくつか紹介いたします。
図形を用いて自然数の和を求める方法
ここでは、
図形を用いる方法
として、
- 石を三角形に並べて求める方法
- 数列を逆から並べて求める方法
の2通りをご紹介いたします。
石を三角形に並べて自然数の和を求める方法
図形を用いるひとつめの方法として
石を三角形に並べて求める方法
をご紹介いたします。
イメージしやすいように
- 最初に、具体的な数列の和を求める
- 次に、一般的な数列の和を求める
といった順番でご紹介いたします。
※「最初は具体的に考えて、その後で一般化・抽象化する」といった手法は、数学の問題を解く際によく使うものなので、頭の隅に置いておくと役に立ちます。
1から5までの自然数の和を求める
ここでは、まず1から5までの自然数の和
\[ 1 + 2 + 3 + 4 + 5 \]
を求めていきます。
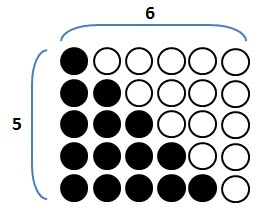
求めたい1から5までの和は、以下のように並べた石の数です。
簡単に和を求めるには、この図を上下ひっくり返したものをくっつけて長方形を作ります。
(ひっくり返したほうを、わかりやすいように白色にしています)
この図からわかるように
縦に5個
横に6個
並んでいますので、石は全部で
\[ 5 \times 6 = 30 \]
です。
同じものをひっくり返して長方形を作ったので、いま求めたい1から5の和は半分の
\( 15 \)個
と求めることができます。

こんなことしなくても、1から5までの和なんて、順番に足していけばいいだろ?
って思った方もおられることでしょう。
しかし、これが1から100までの和ならどうでしょう。また、一般的に1からnまでの和なら?
いま見てきた方法なら、100でもnでも問題ありません。
1からnまでの自然数の和を求める
ここから、1からnまでの自然数の和
\[ 1 + 2 + 3 + \cdots + n \]
も、1から5までの和を求めたときと同じように求めていきます。
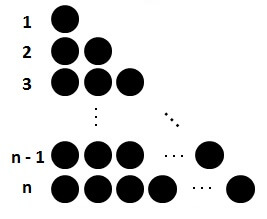
求めたい1からnまでの和は、以下のように並べた石の数です。
この図を上下ひっくり返したものをくっつけて長方形を作ります。
すると
縦にn個
横に(n+1)個
並んでいますので、石は全部で
\( n(n+1) \)個
並んでいます。
いま求めたい1からnの和は、この半分なので
\[ \frac{1}{2}n(n+1) \]
と求めることができます。
数列を逆から並べて自然数の和を求める方法
次の方法は
数を逆から並べて求める方法
です。
ここでも、
- 最初に、具体的な数列の和を求める
- 次に、一般的な数列の和を求める
といった「具体的 → 一般化・抽象化」の流れでご紹介いたします。
まずは、具体的に、1から10までの和と1から11までの和
\begin{align*}
1 + 2 + 3 + \cdots + 10 \\
1 + 2 + 3 + \cdots + 11 \\
\end{align*}
の2つを考えます。
そして、それらを足がかりにして、1からnまでの自然数の和
\[ 1 + 2 + 3 + \cdots + n \]
の公式を導きます。
1から10までの和は?
小学校の頃、次のような問題を親や友達から出されたことはありませんか?
(問題1)
1から10までの和を求めよ(5秒以内)
私は、小学生の頃

5秒以内なんて無理に決まってるやんか!
と言って、問題を出してきた友達とケンカしたことがあります。
普通に足し算を行えば、1から10までの和を求めることはできますが、計算が速い人でないと5秒以内なんて無理ですよね。
でも、ちょっとした”規則性”を見つければ、一瞬で計算できます。
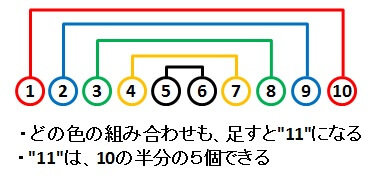
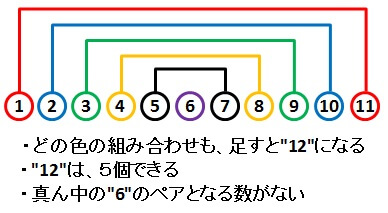
その規則とは、
- 前からn番目と後ろからn番目にある数の和は”11″になる
- 和として出てきた”11″は、10の半分の5個できる
という2点。
言葉ではわかりにくいですが、図で示すと以下のようになります。
その”規則性”を見抜くことができれば、1~10の和は
\[ 11 \times 5 = 55 \]
と一瞬で計算できます。
この方法は、1から10までの和以外にも使えます。
1から100までの和も同じように考えると
- 前からn番目と後ろからn番目にある数の和は”101″になる
- 和として出てきた”101″は、100の半分の50個ある
となりますので
\[ 101 \times 50 = 5050 \]
と簡単に計算できます。
(実際に計算するときは、最初の数”1″と最後の数”100″を足して”101″を求め、個数の”50″をかけると速く計算できます。)
でも、この方法にはひとつ欠点があるのです。
1から11までの和は?
1から10までの和を求めた方法の欠点を見ていくために、次の問題を考えてみてください。
(問題2)
1から11までの和を求めよ(5秒以内)

1から10までの和を求めた方法を使ってみよう!
そう考えて数を並べてみると、1から10の和を求めたときと様子が違うことがわかります。
いちばんの違いは
真ん中の6とペアになる数がない
ということ。
これは、並べた数が1から11までの11個あることが原因です。
奇数個並べると、ちょうど真ん中にくる数が出てきてしまいます。
1から10までの和を求めたときは、並べた数は10個。
偶数個なので、真ん中の数がなく、きれいにペアを組むことができたので、和を簡単に求めることができました。
では、奇数個の場合、どうやって和を求めたらいいでしょうか。
いくつかの方法が考えられます。
- 真ん中の”6″以外の数の和を求めて、最後に”6″を足す
- 1から10までの和を求めて、最後に”11″を足す
- “12”が5.5個あるとして、計算する
しかし、偶数個の場合と奇数個の場合とで求める方法が異なるというのは、なにかと面倒です。
そこで、偶数個でも奇数個でも使える方法はなにかないのか?ということになるのですが、実はうまい方法があるのです。
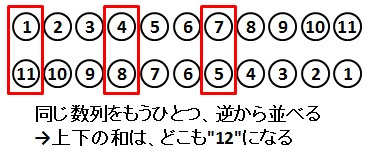
それは、同じ数列をもうひとつ並べることです。しかも逆から。
そうすると、上下に並べられた数の和は、どれも”12″になります。
図を見ると、”12″は、11個あることがわかります。
なので、図に出てきた数をすべて足すと
\[ 12 \times 11 = 132 \]
この”132″は、1から11の和の2倍になっています。(上下に1から11を2つずつ並べたため。)
なので、実際に求めたい1から11の和は
\[ 132 \times \frac{1}{2} = 66 \]
と計算できます。
1からnまでの自然数の和を求める
1からnまでの自然数の和
\[ 1 + 2 + 3 + \cdots + n \]
も同じように求めてみましょう。
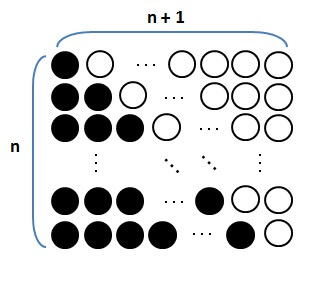
以下の図のように、1からnまでを順番に並べ、さらにその下に1からnまでを逆から並べます。
すると、上下の数の和は、どれもn+1になっていることが確かめられます。
よって、この図には「n+1がn個ある」と考えることができます。
つまり、いま求めたい1からnまでの和は、この半分なので
\[ \frac{1}{2}n(n+1) \]
と表すことができるのです。
階差数列を利用して自然数の和を求める方法
いくつか図形を用いた方法を見てきましたが、ここからは
階差数列を利用して求める方法
をご紹介します。
ここでは、
- \( n \)が階差数列となる数列を計算する方法
- \( n^2 \)の階差数列を使う方法
- \( n^2 \)の階差数列を使う方法
の3つを紹介いたします。
※前提知識として、「階差数列」で紹介している
m次式の数列の階差数列は、(m-1)次式の数列になる
和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる
といったことを用います。
\( n \)が階差数列となる数列を計算する方法
自然数
\[ 1,2,3,\cdots \]
の和を階差数列の考え方を使って求めていきたいと思います。
和を求めるのに必要なものは
階差数列がnとなるような、nの2次式で表される数列
です。
つまり
\[ a_{n+1} – a_n = n \]
となる2次式で表される数列\( \{ a_n \} \)を求めることができれば、1からnまでの和を求めることができるのです。
そこで、階差がnとなるような2次式で表される数列\( \{ a_n \} \)を
\[ a_n = an^2 + bn + c \]
と置くと、その階差数列は
\begin{align*}
& a_{n+1} – a_n \\
= & a(n+1)^2 + b(n+1) + c \\
& – \ (an^2 + bn + c) \\
= & an^2+2an+a + bn+b + c \\
& – an^2 – bn – c \\
= & 2an+ (a + b)
\end{align*}
と計算できます。
いま、階差数列が\( n \)となるような数列を求めたいので
\[ 2an+ (a + b) = n \]
となってほしいのです。
つまり
\begin{cases}
2a = 1 \\
a + b = 0
\end{cases}
となればいいわけです。
これを解くと
\begin{cases}
\displaystyle a = \frac{1}{2} \\
\displaystyle b = – \frac{1}{2}
\end{cases}
となります。
以上より、階差が\( n \)となる数列\( \{ a_n \} \)は
\begin{align*}
a_n & = \frac{1}{2}n^2 – \frac{1}{2}n + c \\
& = \frac{1}{2}(n-1)n + c
\end{align*}
と表せます。
そして、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_n & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、自然数の和は
\begin{align*}
\sum_{k=1}^{n} k & = a_{n+1} – a_1
\end{align*}
となります。
この右辺を計算していくと
\begin{align*}
& a_{n+1} – a_1 \\
= & \frac{1}{2}n(n+1) + c – (\frac{1}{2} \cdot 0 \cdot 1 + c) \\
= & \frac{1}{2}n(n+1)
\end{align*}
となり、1からnまでの和の公式を求めることができます。
\( n^2 \)の階差数列を使う方法
今度は、\( n^2 \)の階差数列を用いた方法で自然数の和を求めてみましょう。
\[ a_n = n^2 \]
の階差数列\( \{ b_n \} \)は
\begin{align*}
b_n & = a_{n+1} – a_n \\
& = (n+1)^2 – n^2 \\
& = n^2 + 2n + 1 – n^2 \\
& = 2n + 1
\end{align*}
と計算できます。
また、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_k & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、いま考えている階差数列\( b_n = 2n + 1 \)の和は
\begin{align*}
\sum_{k=1}^{n} (2k + 1) & = a_{n+1} – a_1
\end{align*}
と表せます。(この式を(1)とします。)
まず、右辺の\( a_{n+1} – a_1 \)は
\begin{align*}
a_{n+1} – a_1 & = (n+1)^2 – 1 \\
& = n^2 + 2n + 1 -1 \\
& = n^2 + 2n
\end{align*}
と計算できます。
一方、左辺の\( \displaystyle \sum_{k=1}^{n} (2k + 1) \)は、「Σ(シグマ)について」でも見たように
\begin{align*}
& \sum_{k=1}^{n} (2k + 1) \\
& = 2 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1
\end{align*}
とΣを分けることができます。
よって、いま考えていた(1)の式は
\begin{align*}
& \sum_{k=1}^{n} (2k + 1) = a_{n+1} – a_1 \\
\Leftrightarrow & 2 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 = n^2 + 2n
\end{align*}
と書き換えることができます。(この式を(2)とします。)
Σの定義を考えると、\( \displaystyle \sum_{k=1}^{n} 1 \)は、1をn回足したものです。
つまり
\[ \sum_{k=1}^{n} 1 = n \]
となりますので、(2)の式は
\begin{align*}
& 2 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 = n^2 + 2n \\
\Leftrightarrow & 2 \sum_{k=1}^{n} k = n^2 + 2n – n \\
\Leftrightarrow & \sum_{k=1}^{n} k = \frac{1}{2} (n^2 + n) \\
\Leftrightarrow & \sum_{k=1}^{n} k = \frac{1}{2} n(n + 1)
\end{align*}
となり、自然数の和の公式を求めることができました。
実は、ここで紹介したのと同じような方法で、
- 2乗の和
- 3乗の和
︙ - m乗の和
を求めることもできるのです。
\( n(n+1) \)の階差数列を使う方法
最後に、連続する自然数の積\( n(n+1) \)という数列の階差数列を用いた方法です。
\[ a_n = n(n+1) \]
の階差数列\( \{ b_n \} \)は
\begin{align*}
b_n & = a_{n+1} – a_n \\
& = (n+1)(n+2) – n(n+1) \\
& = (n+1)\{ (n+2) – n \} \\
& = 2(n+1)
\end{align*}
と計算できます。
また、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_k & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、いま考えている階差数列\( b_n = 2(n+1) \)の和は
\begin{align*}
\sum_{k=1}^{n} 2(k+1) & = a_{n+1} – a_1
\end{align*}
と表せます。(この式を(1)とします。)
まず、右辺の\( a_{n+1} – a_1 \)は
\begin{align*}
a_{n+1} – a_1 & = (n+1)(n+2) – 1 \cdot 2 \\
& = n^2 + 3n + 2 -2 \\
& = n^2 + 3n
\end{align*}
と計算できます。
一方、左辺の\( \displaystyle \sum_{k=1}^{n} 2(k+1) \)は、「Σ(シグマ)について」でも見たように
\begin{align*}
& \sum_{k=1}^{n} 2(k+1) \\
& = 2 \sum_{k=1}^{n} k + 2\sum_{k=1}^{n} 1
\end{align*}
とΣを分けることができます。
よって、いま考えていた(1)の式は
\begin{align*}
& \sum_{k=1}^{n} 2(k+1) = a_{n+1} – a_1 \\
\Leftrightarrow & 2 \sum_{k=1}^{n} k + 2\sum_{k=1}^{n} 1 = n^2 + 3n
\end{align*}
と書き換えることができます。(この式を(2)とします。)
Σの定義を考えると、\( \displaystyle \sum_{k=1}^{n} 1 \)は、1をn回足したものです。
つまり
\[ \sum_{k=1}^{n} 1 = n \]
ですので、(2)の式は
\begin{align*}
& 2 \sum_{k=1}^{n} k + 2\sum_{k=1}^{n} 1 = n^2 + 3n \\
\Leftrightarrow & 2 \sum_{k=1}^{n} k = n^2 + 3n – 2n \\
\Leftrightarrow & \sum_{k=1}^{n} k = \frac{1}{2} (n^2 + n) \\
\Leftrightarrow & \sum_{k=1}^{n} k = \frac{1}{2} n(n + 1)
\end{align*}
となり、自然数の和の公式を求めることができました。