ここでは
\[ 1^2 + 2^2 + 3^2 + \cdots + n^2 \]
といった自然数の2乗の和を扱います。
ここで紹介する1からnまでの2乗の和の公式は、以下のようになります。
\begin{align*}
& 1^2 + 2^2 + 3^2 + \cdots + n^2 \\
= & \frac{1}{6}n(n+1)(2n + 1)
\end{align*}
この公式を、いろんな方法で導いていきます。
最初から全部を理解しようとしなくても大丈夫です。
どれかひとつでも納得できるものがあって、自分で導くことができるようになれば十分です。
「自然数の和」のときと同じように、大きく分けると
- 図形を用いる方法
- 階差数列を利用する方法
のふたつあり、それぞれいくつか紹介いたします。
図形を用いて2乗の和を求める方法
ここでは、
図形を用いる方法
として、
- 石を工夫して並べて求める方法
- 数を正三角形に並べて求める方法
- 数を正方形に並べて求める方法
の3通りをご紹介いたします。
石を工夫して並べて、2乗の和を求める方法
まずひとつめの方法は
石を工夫して並べて求める方法
です。
ここでは、理解しやすいように
- 準備として、奇数の和は平方数になることを見る
- 次に、具体的な数列の和を求める
- 最後に、一般的な数列の和を求める
といった順番でご紹介いたします。
準備:奇数の和は平方数になる
まず、あらかじめ意識しおいてほしいことは
奇数の和は平方数になる
ということ。
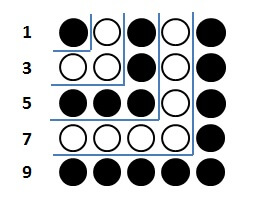
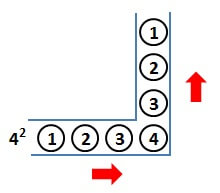
これは、以下の図のように、石を順番にL字に並べてみればひと目でわかります。
1個,3個,5個,…と順番にL字に並べていくと、1辺の長さが1,2,3,…の正方形ができます。
(図は9個までL字に並べて、1辺の長さが5の正方形ができたところ)
1個,3個,5個,7個,9個と石を並べたので、全部で
\[ 1 + 3 + 5 + 7 + 9 = 25 \]
あります。
また、正方形の見方を変えると
縦に5個、横に5個石が並んでいる
と考えられるので
\[ 5^2 = 25 \]
と数えることもできます。
ここから言えるのは
1から順番に奇数を5個並べたとき、その和は\( 5^2 \)になる
ということ。
一般に、1から順番に奇数をn個並べたときも同じように考えられます。
1から順番に数えて、n個目の奇数は、2n-1。
なので、その和は
\[ 1 + 3 + 5 + \cdots + (2n-1) = n^2 \]
となります。
さて、準備が終わったので、ここから2乗の和を求めていきましょう。
1から4までの2乗の和を求める
まずは、具体的に「n = 4の場合」について考えていきます。
つまり
\[ 1^2 + 2^2 + 3^2 + 4^2 \]
を求めていきます。
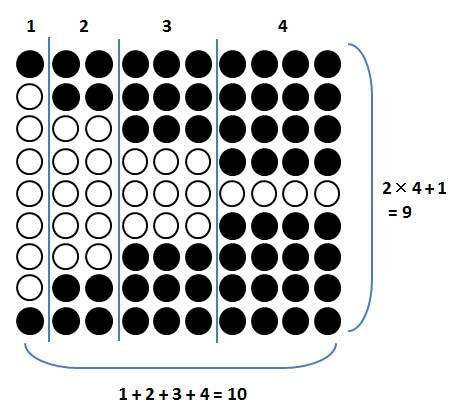
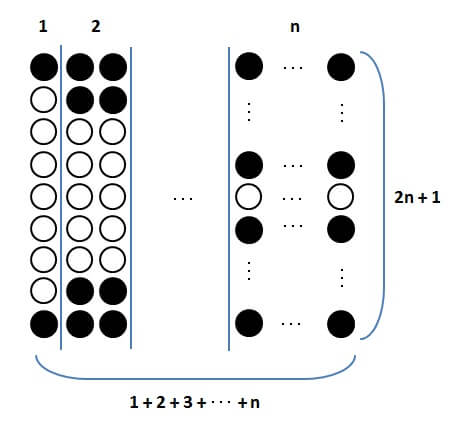
求めたい2乗の和は、以下の図のように並べた●の数です。
これらの石を、以下の図のように、上下反転させてもう1組置きます。
さらに、空いた隙間を○で埋めて大きな長方形を作ります。
このようにして●と○を並べていくと、実は
○の数も、”1から4までの2乗の和”
になっているのです。
それは、準備で見た”奇数の和は平方数になる”ということと大きな関係があるのです。
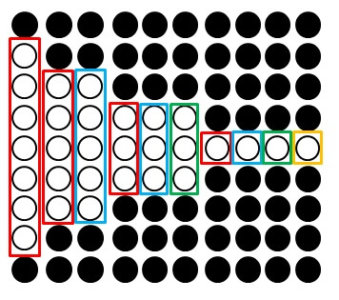
そのことを、以下の図を使って考えていきます。
枠で囲った○は、どれも奇数個あります。
そして、同じ色で囲った○の数を足してみると、どの色で囲ったものも平方数になることがわかります。
実際に、赤枠で囲った○の数を数えてみると
\begin{align*}
7+ 5 + 3 + 1 & = 16 \\
& = 4^2
\end{align*}
青枠で囲った○の数は
\begin{align*}
5 + 3 + 1 & = 9 \\
& = 3^2
\end{align*}
緑の枠で囲った○の数は
\begin{align*}
3 + 1 & = 4 \\
& = 2^2
\end{align*}
黄色の枠で囲った○の数は
\[ 1^2 \]
よって、○の数は全部で
\[ 1^2 + 2^2 + 3^2 + 4^2 \]
個あるのです。
これは、いま求めたい2乗の和の形になっています。
つまり、●と○を並べた大きな長方形には、
2乗の和が3つある
ということです。
そして、図の長方形には
縦:\( (2 \cdot 4 + 1) = 9 \)個
横:\( (1 + 2 + 3 + 4) = 10 \)個
の石が並べられています。
なので、石は全部で
\begin{align*}
& (2 \cdot 4 + 1)(1 + 2 + 3 + 4) \\
= & 9 \cdot 10 \\
= & 90
\end{align*}
個並べられています。
これは、いま求めたい1から4までの2乗の和のちょうど3倍になっています。
ですので、1から4までの2乗の和は
\[ 90 \div 3 = 30 \]
と求めることができます。
1からnまでの2乗の和を求める
今度は、より一般的に1からnまでの2乗の和
\[ 1^2 + 2^2 + 3^2 + \cdots + n^2 \]
を考えます。
n = 4の場合と同じように考えて石を並べていくと
縦:\( (2n + 1) \)個
横:\( (1 + 2 + 3 + 4 + \cdots + n) \)個
の長方形ができます。
ですので、石の数の合計は
\begin{align*}
& ( 2n + 1 )( 1 + 2 + 3 + 4 + \cdots + n ) \\
= & ( 2n + 1 ) \cdot \frac{1}{2}n(n + 1) \\
= & \frac{1}{2}n(n + 1)( 2n + 1 )
\end{align*}
いま求めたい1からnまでの2乗の和は、この\( \frac{1}{3} \)ですので
\[ \frac{1}{6}n(n + 1)( 2n + 1 ) \]
つまり、2乗の和は
\begin{align*}
& 1^2 + 2^2 + 3^2 + \cdots + n^2 \\
& = \frac{1}{6}n(n + 1)( 2n + 1 )
\end{align*}
と導くことができます。
数を正三角形に並べて、2乗の和を求める方法
次にご紹介する方法は
数を正三角形に並べて求める方法
です。
まずは、準備として
\( n^2 \)はnをn回足している
ということを見ます。
その後に、具体的な2乗の和
\[ 1^2 + 2^2 + 3^2 + 4^2 + 5^2 \]
を考え、それを足がかりにして、より一般的な2乗の和
\[ 1^2 + 2^2 + 3^2 + \cdots + n^2 \]
の公式を導きます。
準備:\( n^2 \)はnをn回足している
まず、準備として、考えていただきたいのは
\( n^2 \)は、どういうことを表しているのか?
ということ。
きっと

どういうこともなにも、nを2回かけているだけだろ?
とお思いのことだと思います。
実際
\[ n^2 = n \times n \]
と表されます。
では、さらに掘り下げて
n×nは、どういうことを表してるのでしょうか?
小学校のときに、はじめて掛け算を習ったときのことを思い出してみてください。
たとえば、3×4なら

3を4回足しているんだよ!
と教わったと思います。
この考え方をすると、
n×nは、nをn回足している
ということです。
つまり
\( n^2 \)は、nをn回足している
ということを表しているのです。
式にすると
\[ n^2 = n + n + n + \cdots + n \]
ということです。
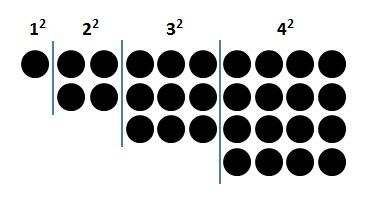
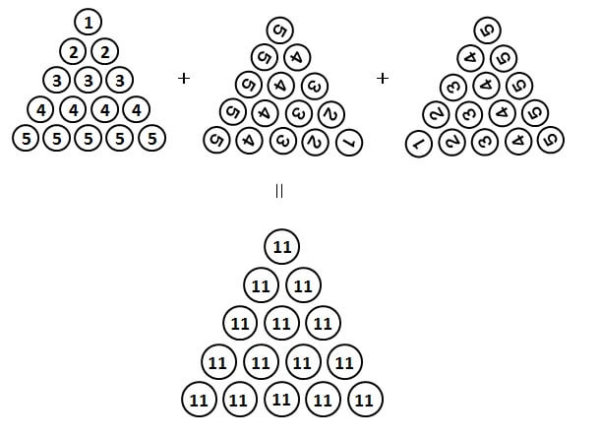
1から5までの2乗の和を求める
まずは、具体的に「n=5の場合」を求めてみましょう。
n=5の場合、求めたい和は
\[ 1^2 + 2^2 + 3^2 + 4^2 + 5^2 \]
です。
準備で見たように
\( 1^2 \)は、1を1回足している(1が1個)
\( 2^2 \)は、2を2回足している(2が2個)
\( 3^2 \)は、3を3回足している(3が3個)
\( 4^2 \)は、4を4回足している(4が4個)
\( 5^2 \)は、5を5回足している(5が5個)
と考えることができます。
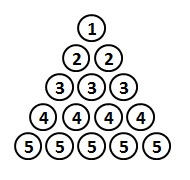
そこで、これらの数字は、以下のように正三角形の形に並べることができます。
求めたいのは、この図に出てくる数の合計です。
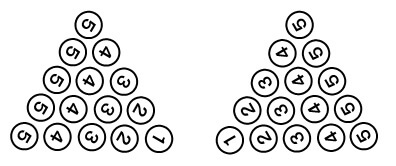
そして、この正三角形に加えて、120°回転したものと240°回転したものを用意します。
そして、これら3つの正三角形において、同じ場所にある数を足してみるとどうなるでしょうか。
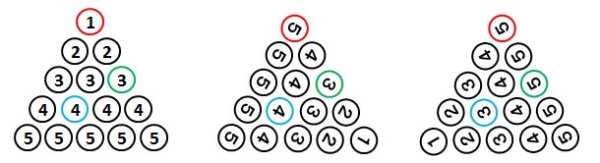
たとえば、上の図では
赤:\( 1 + 5 + 5 = 11 \)
青:\( 4 + 4 + 3 = 11 \)
緑:\( 3 + 3 + 5 = 11 \)
となり、どれも11になります。
他の場所の数でも、和はすべて11になります。
図で表すと、以下のようになります。
この正三角形を見ると、11は
1段目に1個
2段目に2個
3段目に3個
4段目に4個
5段目に5個
並んでいますので、11は全部で
\[1+2+3+4+5 \]
個あります。
よって、11の正三角形に出てくる数の合計は
\begin{align*}
& 11 \times (1+2+3+4+5) \\
= & 11 \times 15 \\
= & 165
\end{align*}
と計算できます。
数字がどれも11の正三角形は、元の正三角形を3つ足してできたものでした。
ですので、求めたい和は
\[ 165 \div 3 = 55 \]
と計算できます。
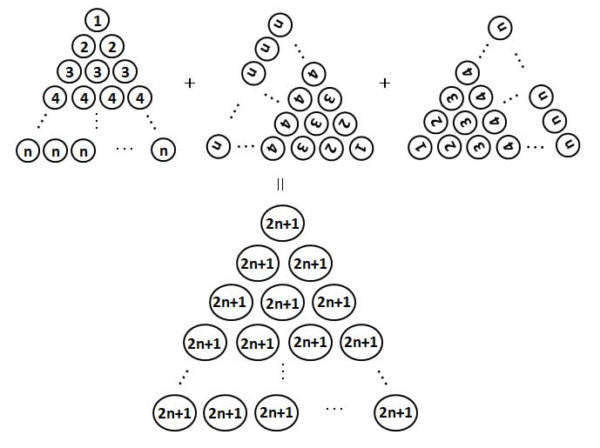
1からnまでの2乗の和を求める
さて、1からnまでの2乗の和も同じように求めていきましょう。
n=5の場合と同じように、120°回転したものと240°回転したものを追加し、同じ場所にある数を足します。
すると、どの場所の和も2n+1になります。
この正三角形には、2n+1が
1段目に1個
2段目に2個
3段目に3個
…
n段目にn個
並んでいますので、2n+1は全部で
\begin{align*}
& 1+2+3+ \cdots + n \\
= & \frac{1}{2}n(n+1)
\end{align*}
個あります。
よって、2n+1の正三角形に出てくる数の合計は
\[ \frac{1}{2}n(n+1)(2n+1) \]
と表すことができます。
この数の\( \frac{1}{3} \)が求めたい1からnの2乗の和なので
\[ \frac{1}{6}n(n+1)(2n+1) \]
と導くことができます。
数を正方形に並べて、2乗の和を求める方法
次にご紹介する方法は
数を正方形に並べて求める方法
です。
まずは、準備として
平方数のもうひとつの表し方
を紹介します。
その後に、具体的な2乗の和
\[ 1^2 + 2^2 + 3^2 + 4^2 + 5^2 \]
を考え、それを足がかりにして、より一般的な2乗の和
\[ 1^2 + 2^2 + 3^2 + \cdots + n^2 \]
の公式を導きます。
準備:平方数のもうひとつの表し方
ひとつめの方法として紹介した「石を工夫して並べて、2乗の和を求める方法」の準備で、
奇数の和は平方数になる
ということは、すでに述べてきました。
実際に計算すると
\[ 1+3+5+7+\cdots+(2n-1) = n^2 \]
となることはすぐに確かめられます。
この奇数の和\( 1+3+5+7+\cdots+(2n-1) \)は、また違った形で表すことができます。
奇数の和は
\begin{align*}
& 1+3+5+7+\cdots+(2n-1) \\
= & 1 + (\underline{1}+2) + (\underline{2}+3) + (\underline{3}+4) \\
& + \cdots + \{\underline{(n-1)}+n \} \\
\end{align*}
と変形でき、下線を引いた部分を式の後ろに持っていき、大きい順番に並び替えると
\begin{align*}
& 1 + 2 + 3 + 4 + \cdots + n \\
& + \underline{(n-1)} + \cdots +\underline{3} + \underline{2} + \underline{1}
\end{align*}
と書き換えることができます。
つまり
\begin{align*}
n^2 = & 1 + 2 + 3 + 4 + \cdots + n \\
& + (n-1) + \cdots + 3 + 2 + 1
\end{align*}
と表せるのです。
この並び方は、あたかも
1,2,3,…と順番にnまで行き、そこからn-1,n-2,…と折り返して再び1まで戻っている
と見え、とてもおもしろい形になっています。
この形を利用すると、1からnまでの2乗の和の公式を導き出すことができます。
1から5までの2乗の和を求める
まずは、具体的に「n = 5の場合」について考えていきます。
つまり
\[ 1^2 + 2^2 + 3^2 + 4^2 + 5^2 \]
を求めていきます。
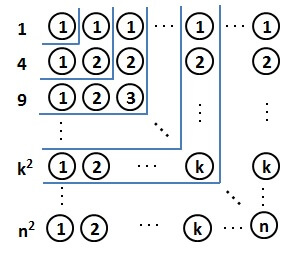
「石を工夫して並べて、2乗の和を求める方法」の”奇数の和は平方数になる”では、石をL字に並べて説明しました。
そして、準備で見てきたように
\begin{align*}
n^2 = & 1 + 2 + 3 + 4 + \cdots + n \\
& + (n-1) + \cdots + 3 + 2 + 1
\end{align*}
と表せることを見ました。
それらのことを考えると、実は、同じようにL字に並べることができるのです。
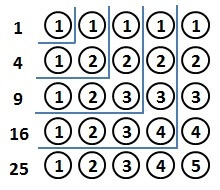
例えば、\( 4^2 \)なら
\[ 1 + 2 + 3 + 4 + 3 + 2 + 1 \]
と表せますので
前半の1から4を右へ
後半の3から1を上へ
並べていくと、以下の図のようになります。
そして
\[ 1^2,2^2,3^2,4^2,5^2 \]
をL字に並べたのが、以下の図です。
L字部分の和がそれぞれ\( 1^2,2^2,3^2,4^2,5^2\)となっていることが確かめられます。
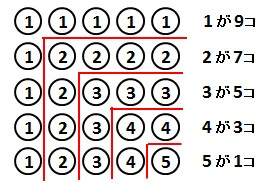
さて、この図の数字の並び方に注目してみてください。
上の図で区切ったL字と逆のL字の形に、同じ数字が並んでいることがわかります。
それぞれの数字の個数を数えると
1が9個
2が7個
3が5個
4が3個
5が1個
あることが確かめられます。
つまり、1から5までの2乗の和は
\begin{align*}
& 1 \cdot 9 + 2 \cdot 7 + 3 \cdot 5 + 4 \cdot 3 + 5 \cdot 1 \\
= & 9 + 14 + 15 + 12 + 5 \\
= & 55
\end{align*}
と計算できます。
1からnまでの2乗の和を求める
この方法で、1からnまでの2乗の和を求めてみましょう。
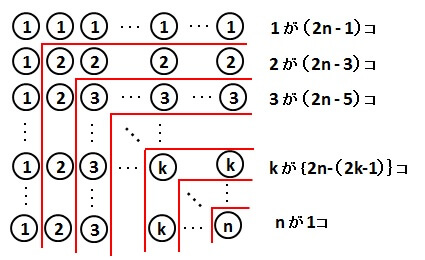
同じように、L字に並べたのが以下の図です。
そして、逆のL字の形で区切った図が以下の通りです。
ここから、それぞれの数字の個数を考えると
1が2n-1個
2が2n-3個
3が2n-5個
…
kが{2n-(2k-1)}個
…
nが1 = 2n-(2n-1)個
あるとわかります。
そのように考えると
\begin{align*}
\sum_{k=1}^{n} k^2 = \sum_{k=1}^{n} k\{2n-(2k-1)\}
\end{align*}
と表すことができます。
この式の右辺について、計算を進めていくと
\begin{align*}
& \sum_{k=1}^{n} k\{2n-(2k-1)\} \\
= & \sum_{k=1}^{n} -2k^2 + (2n+1)k \\
= & -2\sum_{k=1}^{n} k^2 + (2n+1)\sum_{k=1}^{n} k \\
= & -2\sum_{k=1}^{n} k^2 + (2n+1) \cdot \frac{1}{2}n(n+1)
\end{align*}
となります。
つまり
\begin{align*}
& \sum_{k=1}^{n} k^2 = -2 \sum_{k=1}^{n} k^2 + \frac{1}{2}n(n+1)(2n+1) \\
\Leftrightarrow \ & 3 \sum_{k=1}^{n} k^2 = \frac{1}{2}n(n+1)(2n+1) \\
\Leftrightarrow \ & \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1)
\end{align*}
と計算でき、1からnまでの2乗の和を求めることができるのです。
階差数列を利用して、2乗の和を計算する方法
ここまでは、図形を用いた方法で2乗の和を求めてきました。
ここからは
階差数列を利用して2乗の和を求める方法
をご紹介します。
ここでは、
- \( n^2 \)が階差数列となる数列を利用して計算する方法
- \( n^3 \)の階差数列を利用して計算する方法
- \( n(n+1)(n+2) \)の階差数列を利用して計算する方法
の3つを紹介いたします。
※前提知識として、「階差数列」で紹介している
m次式の数列の階差数列は、(m-1)次式の数列になる
和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる
といったことを用います。
\( n^2 \)が階差数列となる数列を利用して計算する方法
1からnまでの2乗の数列
\[ 1^2,2^2,3^2,\cdots \]
の和を、階差数列の考え方を利用して求めます。
和を求めるのに必要なものは
階差数列が\( n^2 \)となるような、nの3次式で表される数列
です。
つまり
\[ a_{n+1} – a_n = n^2 \]
となる3次式で表される数列\( \{ a_n \} \)を求めることができれば、1からnまでの2乗の和を求めることができるということです。
そこで、階差が\( n^2 \)となるような3次式で表される数列\( \{ a_n \} \)を
\[ a_n = an^3 + bn^2 + cn + d \]
と置くと、その階差数列は
\begin{align*}
& a_{n+1} – a_n \\
= & a(n+1)^3 + b(n+1)^2 + c(n+1) + d \\
& – \ (an^3 + bn^2 + cn + d) \\
= & an^3+3an^2+3an + a \\
& + bn^2 + 2bn + b + cn + c + d \\
& – an^3 – bn^2 – cn – d \\
= & 3an^2+3an + a + 2bn + b + c \\
= & 3an^2 + (3a + 2b)n + a + b + c
\end{align*}
と計算できます。
いま階差数列が\( n^2 \)となるような数列を求めたいので
\[ 3an^2 + (3a + 2b)n + a + b + c = n^2 \]
となってほしいのです。
つまり
\begin{cases}
3a = 1 \\
3a + 2b = 0 \\
a + b + c = 0
\end{cases}
となればいいわけです。
これを解くと
\begin{cases}
\displaystyle a = \frac{1}{3} \\
\displaystyle b = – \frac{1}{2} \\
\displaystyle c = \frac{1}{6}
\end{cases}
となります。
以上より、階差が\( n^2 \)となる数列\( \{ a_n \} \)は
\begin{align*}
a_n & = \frac{1}{3}n^3 – \frac{1}{2}n^2 + \frac{1}{6}n + d \\
& = \frac{1}{6}n(2n^2 – 3n + 1) + d \\
& = \frac{1}{6}(n-1)n(2n-1) + d
\end{align*}
と表せます。
そして、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_n & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、2乗の和は
\begin{align*}
\sum_{k=1}^{n} k^2 & = a_{n+1} – a_1
\end{align*}
と表せます。
この右辺を計算していくと
\begin{align*}
& a_{n+1} – a_1 \\
= & \frac{1}{6}n(n+1)(2n+1) + d \\
& – (\frac{1}{6} \cdot 0 \cdot 1 \cdot 1 + d) \\
= & \frac{1}{6}n(n+1)(2n+1)
\end{align*}
となり、1からnまでの2乗の和の公式を求めることができます。
\( n^3 \)の階差数列を利用して計算する方法
次に紹介するのは、いちばん簡単な3次式の数列
\[ a_n = n^3 \]
の階差数列を利用して、2乗の和を求める方法です。
\[ a_n = n^3 \]
の階差数列\( \{ b_n \} \)は
\begin{align*}
b_n & = a_{n+1} – a_n \\
& = (n+1)^3 – n^3 \\
& = n^3 + 3n^2 + 3n + 1 – n^3 \\
& = 3n^2 + 3n + 1
\end{align*}
と計算できます。
また、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_k & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、いま考えている階差数列\( b_n = 3n^2 + 3n + 1 \)の和は
\begin{align*}
\sum_{k=1}^{n} (3k^2 + 3k + 1) & = a_{n+1} – a_1
\end{align*}
と表せます。(この式を(1)とします。)
まず、右辺の\( a_{n+1} – a_1 \)は
\begin{align*}
a_{n+1} – a_1 & = (n+1)^3 – 1 \\
& = n^3 + 3n^2 + 3n + 1 -1 \\
& = n^3 + 3n^2 + 3n
\end{align*}
と計算できます。
一方、左辺の\( \displaystyle \sum_{k=1}^{n} (3k^2 + 3k + 1) \)は、「Σ(シグマ)について」でも見たように
\begin{align*}
& \sum_{k=1}^{n} (3k^2 + 3k + 1) \\
& = 3 \sum_{k=1}^{n} k^2 + 3 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1
\end{align*}
とΣを分けることができます。
よって、いま考えていた(1)の式は
\begin{align*}
& \sum_{k=1}^{n} (3k^2 + 3k + 1) = a_{n+1} – a_1 \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 + 3 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 \\
& = n^3 + 3n^2 + 3n
\end{align*}
と書き換えることができます。(この式を(2)とします。)
Σの定義を考えると、\( \displaystyle \sum_{k=1}^{n} 1 \)は、1をn回足したものです。
つまり
\[ \sum_{k=1}^{n} 1 = n \]
となります。
また、\( \displaystyle \sum_{k=1}^{n} k \)は1からnまでの和なので
\[ \sum_{k=1}^{n} k = \frac{1}{2}n(n+1) \]
となります。
なので、(2)の式は
\begin{align*}
& 3 \sum_{k=1}^{n} k^2 + 3 \sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 \\
&= n^3 + 3n^2 + 3n \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 + \frac{3}{2}n(n+1) + n \\
& = n^3 + 3n^2 + 3n \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 = n^3 + 3n^2 + 3n – (\frac{3}{2}n^2+\frac{5}{2}n) \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 = n^3 + \frac{3}{2}n^2+\frac{1}{2}n \\
\Leftrightarrow & \sum_{k=1}^{n} k^2 = \frac{1}{3}n(n^2 + \frac{3}{2}n + \frac{1}{2}) \\
\Leftrightarrow & \sum_{k=1}^{n} k^2 = \frac{1}{6}n(2n^2 + 3n + 1) \\
\Leftrightarrow & \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n + 1)(2n + 1) \\
\end{align*}
となり、2乗の和の公式を求めることができます。
※教科書や参考書では、2乗の和の公式を導くとき
\[ \sum_{k=1}^n \{ (k+1)^3 – k^3 \} \]
の式がいきなり出てきますが、この式はここまで見てきたように
3次式の階差数列を計算すると、2次式の数列の和を求められるのでは?
という発想があるから思いつく方法ではないでしょうか。
また、ここでひとつ注目してほしいことがあります。
それは、この方法で2乗の和\( \displaystyle \sum_{k=1}^{n} k^2 \)を求める場合
\( \displaystyle \sum_{k=1}^{n} 1 \):0乗の和(1がn個の和)
\( \displaystyle \sum_{k=1}^{n} k \):1乗の和(自然数の和)
が必要になる、ということです。
同様に考えていくと、同じような方法で3乗の和を求める場合には
\( \displaystyle \sum_{k=1}^{n} 1 \):0乗の和(1がn個の和)
\( \displaystyle \sum_{k=1}^{n} k \):1乗の和(自然数の和)
\( \displaystyle \sum_{k=1}^{n} k^2 \):2乗の和
が必要です。
さらに、m乗の和の場合には
\( \displaystyle \sum_{k=1}^{n} 1 \):0乗の和(1がn個の和)
\( \displaystyle \sum_{k=1}^{n} k \):1乗の和(自然数の和)
\( \displaystyle \sum_{k=1}^{n} k^2 \):2乗の和
︙
\( \displaystyle \sum_{k=1}^{n} k^{m-1} \):m – 1乗の和
が必要になってくるのです。
\( n(n+1)(n+2) \)の階差数列を利用して計算する方法
今度は、3つの連続する自然数\( n \)、( n+1 \)、\( n+2 \)の積という形をした数列
\[ n(n+1)(n+2) \]
の階差数列を利用して、2乗の和を求める方法です。
\[ a_n = n(n+1)(n+2) \]
の階差数列\( \{ b_n \} \)は
\begin{align*}
b_n & = a_{n+1} – a_n \\
& = (n+1)(n+2)(n+3) \\
& – n(n+1)(n+2) \\
& = (n+1)(n+2)\{ (n+3) – n \} \\
& = 3(n+1)(n+2)
\end{align*}
と計算できます。
また、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_k & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、いま考えている階差数列\( b_n = 3(n+1)(n+2) \)の和は
\begin{align*}
\sum_{k=1}^{n} 3(k+1)(k+2) & = a_{n+1} – a_1
\end{align*}
と表せます。(この式を(1)とします。)
まず、右辺の\( a_{n+1} – a_1 \)は
\begin{align*}
& a_{n+1} – a_1 \\
& = (n+1)^3 – 1 \\
& = (n+1)(n+2)(n+3) – 1 \cdot 2 \cdot 3 \\
& = (n^2 + 3n +2)(n+3) – 6 \\
& = (n^3 + 3n^2 +2n + 3n^2 + 9n + 6) – 6 \\
& = n^3 + 6n^2 +11n \\
\end{align*}
と計算できます。
一方、左辺の\( \displaystyle \sum_{k=1}^{n} 3(k+1)(k+2) \)は、「Σ(シグマ)について」でも見たように
\begin{align*}
& \sum_{k=1}^{n} 3(k+1)(k+2) \\
& = \sum_{k=1}^{n} 3(k^2 + 3k + 2) \\
& = 3 \sum_{k=1}^{n} k^2 + 3 \sum_{k=1}^{n} k + 2\sum_{k=1}^{n} 1
\end{align*}
とΣを分けることができます。
よって、いま考えていた(1)の式は
\begin{align*}
& \sum_{k=1}^{n} 3(k+1)(k+2) = a_{n+1} – a_1 \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 + 9 \sum_{k=1}^{n} k + 6\sum_{k=1}^{n} 1 \\
& = n^3 + 6n^2 +11n
\end{align*}
と書き換えることができます。(この式を(2)とします。)
Σの定義を考えると、\( \displaystyle \sum_{k=1}^{n} 1 \)は、1をn回足したものです。
つまり
\[ \sum_{k=1}^{n} 1 = n \]
となります。
また、\( \displaystyle \sum_{k=1}^{n} k \)は1からnまでの和なので
\[ \sum_{k=1}^{n} k = \frac{1}{2}n(n+1) \]
となります。
なので、(2)の式は
\begin{align*}
& 3 \sum_{k=1}^{n} k^2 + 9 \sum_{k=1}^{n} k + 6 \sum_{k=1}^{n} 1 \\
& = n^3 + 6n^2 +11n \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 + \frac{9}{2}n(n+1) + 6n \\
& = n^3 + 6n^2 +11n \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 \\
& = n^3 + 6n^2 +11n – (\frac{9}{2}n^2+\frac{21}{2}n) \\
\Leftrightarrow & 3 \sum_{k=1}^{n} k^2 = n^3 + \frac{3}{2}n^2+\frac{1}{2}n \\
\Leftrightarrow & \sum_{k=1}^{n} k^2 = \frac{1}{3}n(n^2 + \frac{3}{2}n + \frac{1}{2}) \\
\Leftrightarrow & \sum_{k=1}^{n} k^2 = \frac{1}{6}n(2n^2 + 3n + 1) \\
\Leftrightarrow & \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n + 1)(2n + 1) \\
\end{align*}
となり、2乗の和の公式を求めることができます。
任意の3次式の階差数列を利用して計算してみる
(掲載準備中)
自然数の和と比較して導き出す方法
(掲載準備中)