ここでは
\[ 1^3 + 2^3 + 3^3 + \cdots + n^3 \]
といった自然数の3乗の和を扱います。
ここで紹介する1からnまでの3乗の和の公式は、以下のようになります。
\begin{align*}
& 1^3 + 2^3+ 3^3 + \cdots + n^3 \\
= & \frac{1}{4}n^2(n+1)^2 \\
= & \{ \frac{1}{2}n(n+1) \}^2
\end{align*}
この公式を、いろんな方法で導いていきます。
最初から全部を理解しようとしなくても大丈夫です。
どれかひとつでも納得できるものがあって、自分で導くことができるようになれば十分です。
「自然数の和」や「2乗の和」のときと同じように、大きく分けると
- 図形を用いる方法
- 階差数列を利用する方法
のふたつあり、それぞれいくつか紹介いたします。
図形を用いて3乗の和を求める方法
ここでは、
図形を用いる方法
として、
- 石を工夫して並べて求める方法
- 数を正方形に並べて求める方法
- 数を立体的に並べて、3乗の和を求める方法
の3通りをご紹介いたします。
石を工夫して並べて、3乗の和を求める方法
まずひとつめの方法は
石を工夫して並べて求める方法
です。
まずは、具体的な3乗の和
\[ 1^3 + 2^3 + 3^3 + 4^3 \]
を考え、それを足がかりにして、より一般的な3乗の和
\[ 1^3 + 2^3 + 3^3 + \cdots + n^3 \]
の公式を導きます。
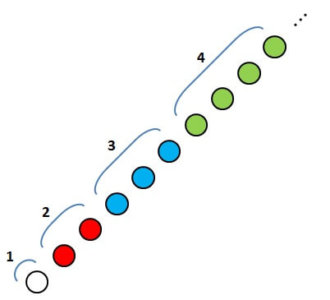
1から4までの3乗の和を求める
ここでは、一風変わった並べ方で1から4までの3乗の和
\[ 1^3 + 2^3 + 3^3 + 4^3 \]
を求めていきます。
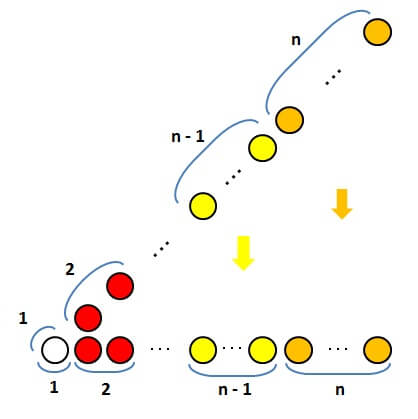
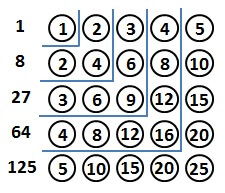
まず、以下の図のように、斜めに1,2,3,…と石を並べます。
そこから、左と下に向かって、等間隔に石を並べていきます。
4まで斜めに並べた場合、以下のようになります。
このように並べたとき、各色の石の数は、立方数(3乗の数)になっているのです。
実際に数えてみると
白:1個
赤:8個
青:27個
緑:64個
と、それぞれ\( 1^3,2^3,3^3,4^3 \)となっています。
つまり、上の図に出てくる石の数は
\[ 1^3 + 2^3 + 3^3 + 4^3 \]
あります。
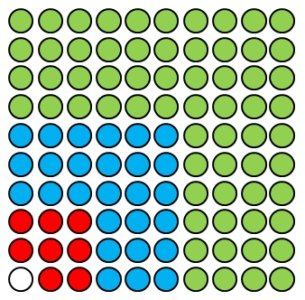
一方で、上の図は
縦に\( 1 + 2 + 3 + 4 = 10 \)個
横に\( 1 + 2 + 3 + 4 = 10 \)個
並べた正方形の形をしています。
つまり、石は全部で
\[ 10 \times 10 = 100 \]
あると計算できます。
以上より
\[ 1^3 + 2^3 + 3^3 + 4^3 = 100 \]
と求めることができるのです。
1からnまでの3乗の和を求める
ここまで、4個まで斜めに並べて、1から4までの3乗の和を求めました。

でも、n個並べたときも、本当に\( n^3 \)個並んでいるの?
とお思いの方もおられると思いますので、斜めにn個並べたときに\( n^3 \)個並べられることを確かめていきましょう。
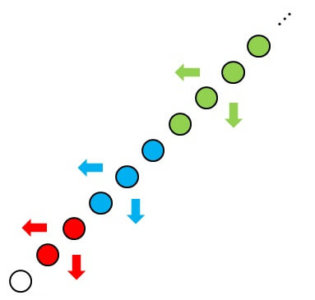
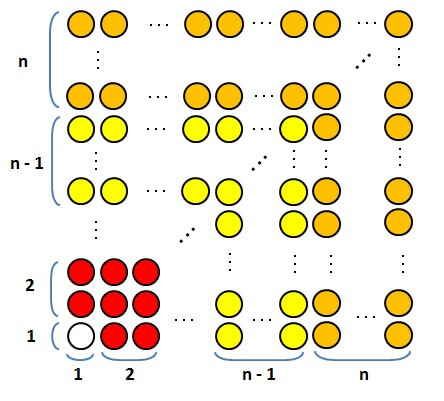
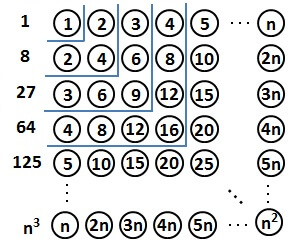
まず、斜めにnまで並べ、下方向に石を並べたときを考えてみましょう。
ここから下方向に石を並べていくのですが、注目していただきたいのが
いちばん下の列には、石が何個並んでいるか?
ということ。
以下の図のように考えるとわかるように、いちばん下の列の石の数は全部で
\[ 1 + 2 + \cdots + (n-1) + n \]
と表せます。
これは、左方向に石を並べていったときも同様です。
さて、このように並べたとき、斜めにn個並べたところから作ったオレンジの石は、全部でいくつあるでしょうか。
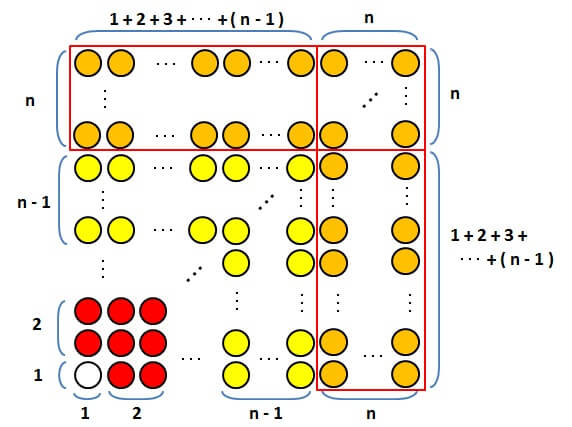
数えるために、以下の図のようにひとつの正方形とふたつの長方形とに分けて考えます。
このように分けたとき、長方形ひとつあたり
\begin{align*}
& \{1+2+\cdots + (n-1)\} \cdot n \\
= & \frac{1}{2}(n-1)n^2
\end{align*}
だけ石が並んでいます。
一方、正方形の部分には
\[ n^2 \]
だけ石が並んでいます。
ですので、オレンジの石は全部で
\begin{align*}
& 2 \cdot \frac{1}{2}(n-1)n^2 + n^2 \\
= & n^3 – n^2 + n^2 \\
= & n^3
\end{align*}
となります。
よって、斜めにn個並べたときに\( n^3 \)個並べられることを確かめることができました。
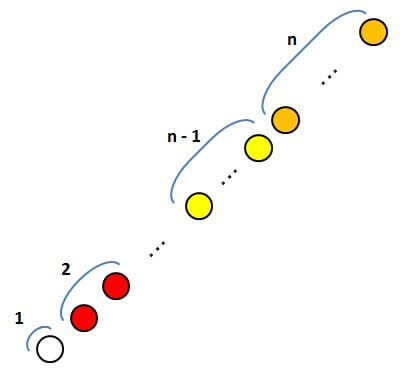
つまり、ここまで見てきたような石の並べ方をすると、各色の石の数はそれぞれ
\[ 1^3 ,2^3 ,3^3,\cdots ,(n-1)^3,n^3 \]
だけあり、1辺に
\begin{align*}
& 1+2+3+\cdots+(n-1)+n \\
= & \frac{1}{2}n(n+1)
\end{align*}
だけ石が並んでいる正方形ができるのです。
そして、石の数は全部で
\[ \{ \frac{1}{2}n(n+1) \}^2 \]
と数えることができます。
以上より、いま求めたい1からnまでの3乗の和は
\begin{align*}
& 1^3+2^3+3^3+\cdots+(n-1)^3+n^3 \\
= & \{ \frac{1}{2}n(n+1) \}^2
\end{align*}
となるのです。
数を正方形に並べて、3乗の和を求める方法
次の方法は
数を正方形に並べて求める方法
です。
まずは、準備として
立方数の別の表し方
を紹介します。
その後に、具体的な3乗の和
\[ 1^3 + 2^3 + 3^3 + 4^3 + 5^3 \]
を考え、それを足がかりにして、より一般的な3乗の和
\[ 1^3 + 2^3 + 3^3 + \cdots + n^3 \]
の公式を導きます。
準備:立方数のもうひとつの表し方
「2乗の和」では、和を求める方法のひとつとして
数を正方形に並べて、2乗の和を求める方法
をご紹介しました。
そこでは、準備の「平方数のもうひとつの表し方」のところで
\begin{align*}
n^2 = & 1 + 2 + 3 + 4 + \cdots + n \\
& + (n-1) + \cdots + 3 + 2 + 1
\end{align*}
と表せることを見ました。
そのことを使うと、立方数(3乗の数)もおもしろい形で表現することができます。
実際
\begin{align*}
n^3 = & n \cdot n^2 \\
= & n (1 + 2 + 3 + 4 + \cdots + n \\
& + (n-1) + \cdots + 3 + 2 + 1) \\
= & n + 2n + 3n + 4n + \cdots + n^2 \\
& + (n-1)n + \cdots + 3n + 2n + n)
\end{align*}
と表すことができ、あたかも
n,2n,3n,…と順番にn^2まで行き、そこから(n-1)n,(n-2)n,…と折り返して再びnまで戻っている
ように見ることができるのです。
1から5までの3乗の和を求める
さて、まずは1から5までの3乗の和
\[ 1^3 + 2^3 + 3^3 + 4^3 + 5^3 \]
を考えていきましょう。
準備でみたように、\( n^3 \)は折り返したような形で表すこともできます。
そして、「数を正方形に並べて、2乗の和を求める方法」でL字に並べたように、\( n^3 \)も同じようにL字に並べることができるのです。
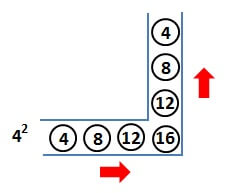
例えば、\( 4^3 \)なら
\[ 4 + 4 \cdot 2 + 4 \cdot 3 + 4 \cdot 4 + 4 \cdot 3 + 4 \cdot 2 + 4 \cdot 1 \]
と表せますので
前半の\( 4 \)から\( 4 \cdot 4 \)を右へ
後半の\( 4 \cdot 3 \)から\( 4 \)を上へ
並べていくと、以下の図のようになります。
そして、1から5までの3乗
\[ 1^3,2^3,3^3,4^3,5^3 \]
をL字に並べたのが、以下の図です。
L字部分の和がそれぞれ\( 1^3,2^3,3^3,4^3,5^3\)となっていることが確かめられます。
さて、この図の数字を横に見てみると
1段目:\( 1,2,3,4,5 \)
2段目:\( 2,4,6,8,10 \)
3段目:\( 3,6,9,12,15 \)
4段目:\( 4,8,12,16,20 \)
5段目:\( 5,10,15,20,25 \)
と並んでいることが確かめられます。
つまり、それぞれの段に並んでいる数の合計は
1段目:\( 1+2+3+4+5 \)
2段目:\( 2+4+6+8+10 \)
3段目:\( 3+6+9+12+15 \)
4段目:\( 4+8+12+16+20 \)
5段目:\( 5+10+15+20+25 \)
と表せます。
よって、この図に出てくる数の和は
\begin{align*}
& 1+2+3+4+5 \\
& + 2+4+6+8+10 \\
& + 3+6+9+12+15 \\
& + 4+8+12+16+20 \\
& + 5+10+15+20+25 \\
= & 1+2+3+4+5 \\
& + 2(1+2+3+4+5) \\
& + 3(1+2+3+4+5) \\
& + 4(1+2+3+4+5) \\
& + 5(1+2+3+4+5) \\
= & (1+2+3+4+5)(1+2+3+4+5) \\
= & (1+2+3+4+5)^2 \\
= & 15^2 \\
= & 225
\end{align*}
と計算することができます。
つまり
\begin{align*}
& 1^3 + 2^3 + 3^3 + 4^3 + 5^3 \\
= & 225
\end{align*}
ということがわかります。
1からnまでの3乗の和を求める
この方法で、1からnまでの3乗の和を求めてみましょう。
同じように、L字に並べたのが以下の図です。
さて、1から5までのときと同じように横に見てみると
1段目:\( 1,2,3,\cdots ,n \)
2段目:\( 2,4,6,\cdots ,2n \)
3段目:\( 3,6,9,\cdots ,3n \)
…
n段目:\( n,2n,3n,\cdots ,n^2 \)
となっていることが確かめられます。
よって、1からnまでの3乗の和は
\begin{align*}
& 1+2+3+\cdots+n \\
& + 2+4+6+\cdots+2n \\
& + 3+6+9+\cdots+3n \\
& + \cdots \\
& + n+2n+3n+\cdots+n^2 \\
= & 1+2+3+\cdots+n \\
& + 2(1+2+3+\cdots+n) \\
& + 3(1+2+3+\cdots+n) \\
& + \cdots \\
& + n(1+2+3+\cdots+n) \\
= & (1+2+3+\cdots+n)(1+2+3+\cdots+n) \\
= & (1+2+3+\cdots+n)^2 \\
= & \{ \frac{1}{2}n(n+1) \}^2
\end{align*}
と計算することができます。
数を立体的に並べて、3乗の和を求める方法
(掲載準備中)
階差数列を利用して、3乗の和を求める方法
ここまでは、図形を用いた方法で3乗の和を求めてきました。
ここからは
階差数列を利用して3乗の和を求める方法
をご紹介します。
ここでは、
- \( n^3 \)が階差数列となる数列を利用して計算する方法
- \( n^4 \)の階差数列を利用して計算する方法
- \( n(n+1)(n+2)(n+3) \)の階差数列を利用して計算する方法
の3つを紹介いたします。
※前提知識として、「階差数列」で紹介している
m次式の数列の階差数列は、(m-1)次式の数列になる
和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる
といったことを用います。
\( n^3 \)が階差数列になる数列を利用して計算する方法
1からnまでの3乗の数列
\[ 1^3,2^3,3^3,\cdots \]
の和を、階差数列の考え方を利用して求めます。
和を求めるのに必要なものは
階差数列が\( n^3 \)となるような、nの4次式で表される数列
です。
つまり
\[ a_{n+1} – a_n = n^3 \]
となる4次式で表される数列\( \{ a_n \} \)を求めることができれば、1からnまでの3乗の和を求めることができるのです。
そこで、階差がnとなるような4次式で表される数列\( \{ a_n \} \)を
\[ a_n = an^4 + bn^3 + cn^2 + dn + e \]
と置くと、その階差数列は
\begin{align*}
& a_{n+1} – a_n \\
= & a(n+1)^4 + b(n+1)^3 + c(n+1)^2 \\
& + d(n+1) + e \\
& – \ (an^4 + bn^3 + cn^2 + dn + e) \\
= & an^4+4an^3+6an^2 + 4an + a \\
& + bn^3 + 3bn^2 + 3bn + b \\
& + cn^2 + 2cn + c \\
& + dn + d + e \\
& – an^4 – bn^3 – cn^2 – dn – e \\
= & 4an^3+6an^2 + 4an + a \\
& + 3bn^2 + 3bn + b \\
& + 2cn + c + d \\
= & 4an^3+3(2a+b)n^2 \\
& + (4a + 3b +2c)n + a+b+c+d
\end{align*}
と計算できます。
いま階差数列が\( n^3 \)となるような数列を求めたいので
\begin{align*}
& 4an^3+3(2a+b)n^2 \\
& + (4a + 3b +2c)n + a+b+c+d \\
= & n^3
\end{align*}
つまり
\begin{cases}
4a = 1 \\
2a+b = 0 \\
4a + 3b +2c = 0 \\
a+b+c+d = 0
\end{cases}
となればいいわけです。
これを解くと
\begin{cases}
\displaystyle a = \frac{1}{4} \\
\displaystyle b = – \frac{1}{2} \\
\displaystyle c = \frac{1}{4} \\
d = 0
\end{cases}
となります。
以上より、階差が\( n^3 \)となる数列\( \{ a_n \} \)は
\begin{align*}
a_n & = \frac{1}{4}n^4 – \frac{1}{2}n^3 + \frac{1}{4}n^2 + e \\
& = \frac{1}{4}n^2(n^2 – 2n + 1) + e \\
& = \frac{1}{4}n^2(n-1)^2 + e
\end{align*}
と表せます。
そして、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_n & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、3乗の和は
\begin{align*}
\sum_{k=1}^{n} k^3 & = a_{n+1} – a_1
\end{align*}
と表せます。
これを計算していくと
\begin{align*}
& a_{n+1} – a_1 \\
= & \frac{1}{4}n^2(n+1)^2 + e \\
& – (\frac{1}{4} \cdot 0^2 \cdot 1^2 + e) \\
= & \frac{1}{4}n^2(n+1)^2 \\
= & \{\frac{1}{2}n(n+1) \}^2
\end{align*}
となり、1からnまでの3乗の和の公式を求めることができます。
(ちなみに、この3乗の和の公式は、”自然数の和の公式の2乗”という形をしています。)
\( n^4 \)の階差数列を利用して計算する方法
次は、いちばん簡単な4次式の数列
\[ a_n = n^4 \]
の階差数列を利用して、3乗の和を求める方法です。
\[ a_n = n^4 \]
の階差数列\( \{ b_n \} \)は
\begin{align*}
b_n & = a_{n+1} – a_n \\
& = (n+1)^4 – n^4 \\
& = n^4 + 4n^3 + 6n^2 + 4n + 1 – n^4 \\
& = 4n^3 + 6n^2 + 4n + 1
\end{align*}
と計算できます。
また、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_k & = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、いま考えている階差数列\( b_n = 4n^3 + 6n^2 + 4n + 1 \)の和は
\begin{align*}
\sum_{k=1}^{n} (4k^3 + 6k^2 + 4k + 1) & = a_{n+1} – a_1
\end{align*}
と表せます。(この式を(1)とします。)
まず、右辺の\( a_{n+1} – a_1 \)は
\begin{align*}
a_{n+1} – a_1 & = (n+1)^4 – 1 \\
& = n^4 + 4n^3 + 6n^2 + 4n + 1 -1 \\
& = n^4 + 4n^3 + 6n^2 + 4n
\end{align*}
と計算できます。
一方、左辺の\( \displaystyle \sum_{k=1}^{n} (4k^3 + 6k^2 + 4k + 1) \)は、「Σ(シグマ)について」でも見たように
\begin{align*}
& \sum_{k=1}^{n} (4k^3 + 6k^2 + 4k + 1) \\
& = 4 \sum_{k=1}^{n} k^3 + 6 \sum_{k=1}^{n} k^2 + 4\sum_{k=1}^{n} k + \sum_{k=1}^{n} 1
\end{align*}
とΣを分けることができます。
よって、いま考えていた(1)の式は
\begin{align*}
& \sum_{k=1}^{n} (4k^3 + 6k^2 + 4k + 1) = a_{n+1} – a_1 \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 6 \sum_{k=1}^{n} k^2 + 4\sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 \\
& = n^4 + 4n^3 + 6n^2 + 4n
\end{align*}
と書き換えることができます。(この式を(2)とします。)
Σの定義を考えると、\( \displaystyle \sum_{k=1}^{n} 1 \)は、1をn回足したものです。
つまり
\[ \sum_{k=1}^{n} 1 = n \]
となります。
また、\( \displaystyle \sum_{k=1}^{n} k \)は1からnまでの和なので
\[ \sum_{k=1}^{n} k = \frac{1}{2}n(n+1) \]
\( \displaystyle \sum_{k=1}^{n} k^2 \)は2乗の和なので
\[ \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1) \]
なので、(2)の式は
\begin{align*}
& 4 \sum_{k=1}^{n} k^3 + 6 \sum_{k=1}^{n} k^2 + 4\sum_{k=1}^{n} k + \sum_{k=1}^{n} 1 \\
& = n^4 + 4n^3 + 6n^2 + 4n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + n(n+1)(2n+1) \\
& + 2n(n+1) + n \\
& = n^4 + 4n^3 + 6n^2 + 4n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 2n^3 + 3n^2 + n \\
& + 2n^2 + 2n + n \\
& = n^4 + 4n^3 + 6n^2 + 4n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 2n^3 + 5n^2 + 4n \\
& = n^4 + 4n^3 + 6n^2 + 4n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 \\
& = n^4 + 4n^3 + 6n^2 + 4n \\
& – (2n^3 + 5n^2 + 4n) \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 = n^4 + 2n^3 + n^2 \\
\Leftrightarrow & \sum_{k=1}^{n} k^3 = \frac{1}{4} n^2(n + 2n + 1) \\
\Leftrightarrow & \sum_{k=1}^{n} k^3 = \frac{1}{4} n^2(n + 1)^2 \\
\Leftrightarrow & \sum_{k=1}^{n} k^3 = \{ \frac{1}{2} n(n + 1) \}^2 \\
\end{align*}
となり、3乗の和の公式を求めることができます。
※教科書や参考書では、3乗の和の公式を導くとき
\[ \sum_{k=1}^n \{ (k+1)^4 – k^4 \} \]
の式がいきなり出てきますが、この式はここまで見てきたように
4次式の階差数列を計算すると、3次式の数列の和を求められるのでは?
という発想があるから思いつく方法ではないでしょうか。
また、2乗の和の場合と同様に、この方法で3乗の和を求める場合
- \( \displaystyle \sum_{k=1}^{n} 1 \):0乗の和(1がn個の和)
- \( \displaystyle \sum_{k=1}^{n} k \):1乗の和(自然数の和)
- \( \displaystyle \sum_{k=1}^{n} k^2 \):2乗の和
が必要になる、ということです。
2乗の和の公式を求めた場合と比較するとわかるように、これは、m乗の和をこの方法で求める場合
- 0乗の和
- 1乗の和
… - (m-1)乗の和
が必要になる、ということです。
\( n(n+1)(n+2)(n+3)\)の階差数列をを利用して計算する方法
4つの連続する自然数\( n \)と\( n+1 \)、\( n+2 \)、\( n+3 \)の積という形をした数列
\[ n(n+1)(n+2)(n+3) \]
の階差数列を利用して、3乗の和を求める方法です。
\[ a_n = n(n+1)(n+2)(n+3) \]
の階差数列\( \{ b_n \} \)は
\begin{align*}
b_n = & a_{n+1} – a_n \\
= & (n+1)(n+2)(n+3)(n+4) \\
& – n(n+1)(n+2)(n+3) \\
= & (n+1)(n+2)(n+3)\{ (n+4) – n \} \\
= & 4(n+1)(n+2)(n+3)
\end{align*}
と計算できます。
また、「和を求めたい数列が階差数列となるような数列を見つければ、和は計算できる」でも見たように、階差数列の和は
\begin{align*}
\sum_{k=1}^{n} b_k = a_{n+1} – a_1
\end{align*}
と表せます。
つまり、いま考えている階差数列\( b_n = 4(n+1)(n+2)(n+3) \)の和は
\begin{align*}
\sum_{k=1}^{n} 4(k+1)(k+2)(k+3) = a_{n+1} – a_1
\end{align*}
と表せます。(この式を(1)とします。)
まず、右辺の\( a_{n+1} – a_1 \)は
\begin{align*}
& a_{n+1} – a_1 \\
= & (n+1)(n+2)(n+3)(n+4) \\
& – 1 \cdot 2 \cdot 3 \cdot 4\\
= & (n^2+3n+2)(n+3)(n+4) -24 \\
= & (n^3+3n^2+2n + 3n^2+9n+6)(n+4) \\
& -24 \\
= & (n^3+6n^2+11n+6)(n+4) -24 \\
= & n^4+6n^3+11n^2+6n \\
& + 4n^3+24n^2+44n+24 -24 \\
= & n^4+10n^3+35n^2+50n \\
\end{align*}
と計算できます。
一方、左辺の\( \displaystyle \sum_{k=1}^{n} 4(k+1)(k+2)(k+3) \)は、「Σ(シグマ)について」でも見たように
\begin{align*}
& \sum_{k=1}^{n} 4(k+1)(k+2)(k+3) \\
= & 4 \sum_{k=1}^{n} (k^2 + 3k +2)(k+3) \\
= & 4 \sum_{k=1}^{n} (k^3 + 3k^2 +2k + 3k^2 + 9k +6) \\
= & 4 \sum_{k=1}^{n} (k^3 + 6k^2 + 11k + 6) \\
= & 4 \sum_{k=1}^{n} k^3 + 24 \sum_{k=1}^{n} k^2 \\
& + 44 \sum_{k=1}^{n} k + 24 \sum_{k=1}^{n} 1
\end{align*}
とΣを分けることができます。
よって、いま考えていた(1)の式は
\begin{align*}
& \sum_{k=1}^{n} 4(k+1)(k+2)(k+3) = a_{n+1} – a_1 \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 24 \sum_{k=1}^{n} k^2 + 44 \sum_{k=1}^{n} k + 24 \sum_{k=1}^{n} 1 \\
& = n^4+10n^3+35n^2+50n
\end{align*}
と書き換えることができます。(この式を(2)とします。)
Σの定義を考えると、\( \displaystyle \sum_{k=1}^{n} 1 \)は、1をn回足したものです。
つまり
\[ \sum_{k=1}^{n} 1 = n \]
となります。
また、\( \displaystyle \sum_{k=1}^{n} k \)は1からnまでの和なので
\[ \sum_{k=1}^{n} k = \frac{1}{2}n(n+1) \]
\( \displaystyle \sum_{k=1}^{n} k^2 \)は2乗の和なので
\[ \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1) \]
なので、(2)の式は
\begin{align*}
& 4 \sum_{k=1}^{n} k^3 + 24 \sum_{k=1}^{n} k^2 \\
& + 44 \sum_{k=1}^{n} k + 24 \sum_{k=1}^{n} 1 \\
& = n^4+10n^3+35n^2+50n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 4n(n+1)(2n+1) \\
& + 22n(n+1) + 24n \\
& = n^4+10n^3+35n^2+50n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 4n(2n^2+3n +1)\\
& + 22n^2 + 22n + 24n \\
& = n^4+10n^3+35n^2+50n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 8n^3+12n^2 +4n \\
& + 22n^2 + 46n \\
& = n^4+10n^3+35n^2+50n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 + 8n^3+34n^2 +50n \\
& = n^4+10n^3+35n^2+50n \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 \\
& = n^4+10n^3+35n^2+50n \\
& – (8n^3+34n^2 +50n) \\
\Leftrightarrow & 4 \sum_{k=1}^{n} k^3 = n^4 + 2n^3 + n^2 \\
\Leftrightarrow & \sum_{k=1}^{n} k^3 = \frac{1}{4} n^2(n + 2n + 1) \\
\Leftrightarrow & \sum_{k=1}^{n} k^3 = \frac{1}{4} n^2(n + 1)^2 \\
\Leftrightarrow & \sum_{k=1}^{n} k^3 = \{ \frac{1}{2} n(n + 1) \}^2 \\
\end{align*}
となり、3乗の和の公式を求めることができます。
任意の4次式の数列の階差数列を利用して計算してみる
(掲載準備中)
自然数の和と比較して導き出す方法
(掲載準備中)